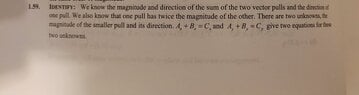Two workers pull horizontally on a heavy box

[rstor]

Homework Statement

Two workers pull horizontally on a heavy box, but one pulls twice as hard as the other. The larger pull is directed at 21.0 degrees west of north, and the resultant of these two pulls is 460.0N directly northward. Use vector components to find the magnitude of each of these pulls and the direction of the smaller pull.

Relevant Equations

$A_x+B_x = C_x$

My solution for finding the direction of the smaller pull is slightly off from the text solution. I am unsure why.

Assuming the larger vector is $\vec B$, the smaller $\vec A$, and the resultant $\vec C$. My solution for the direction of this smaller pull (for the smaller pull in quadrant one) is as follows:

My solution:
$A_x+B_x = C_x$
$| \vec A |cos \phi + 2| \vec A | cos111° = 0$
$| \vec A |(cos \phi + 2cos111°) = 0$
From zero product property
$cos \phi + 2cos111° = 0$
$\phi = 44.21°$

Text book solution:
$2| \vec A |sin21.0° = | \vec A |sin\phi$
$\phi = 45.79°$

I do not understand why there is a difference.

 

[erobz]

I think the textbook solution is not correct.

Should be:

$$ 2 |\vec{F}| \sin \left( 21^{\circ} \right) = |\vec{F}| \cos \left( \phi \right) $$

 

[kuruman]

I think the textbook solution is not correct.

Should be:

$$ 2 |\vec{F}| \sin \left( 21^{\circ} \right) = |\vec{F}| \cos \left( \phi \right) $$

You preempted me, but I agree.

 

[rstor]

Your answers had me look back to the solution manual. It defines the angle $/phi$ between the terminal arm and the y-axis for vector A (and states the answer as 45.8 degrees east of north) whereas I was looking at $/phi$ between the initial side and the terminal arm of vector A.

Thank you all!

 

[kuruman]

Your answers had me look back to the solution manual. It defines the angle $/phi$ between the terminal arm and the y-axis for vector A (and states the answer as 45.8 degrees east of north) whereas I was looking at $/phi$ between the initial side and the terminal arm of vector A.

Thank you all!

You're welcome. Next time please post any figure(s) associated with the statement of the problem. It will make everybody's task easier. Thanks.

 

[haruspex]

Your answers had me look back to the solution manual. It defines the angle $/phi$ between the terminal arm and the y-axis for vector A (and states the answer as 45.8 degrees east of north) whereas I was looking at $/phi$ between the initial side and the terminal arm of vector A.

Thank you all!

To get the LaTeX to work, use \ instead of /.

 

[rstor]

I am still having problems with this question. There is no diagram provided in the original question, however I have attached the diagram from the student solution manual. Continuing from my first post, I understand that one possible solution is $\vec A$ having a direction of $45.8°$ east of north.

For the case where $\vec A$ is in the fourth quadrant, I do not understand how they arrive at $\phi = 45.8°$ south of east. Should it not be $\phi = 44.2°$ south of east?

 

[erobz]

I am still having problems with this question. There is no diagram provided in the original question, however I have attached the diagram from the student solution manual. Continuing from my first post, I understand that one possible solution is $\vec A$ having a direction of $45.8°$ east of north.

For the case where $\vec A$ is in the fourth quadrant, I do not understand how they arrive at $\phi = 45.8°$ south of east. Should it not be $\phi = 44.2°$ south of east?

I think you are getting mixed up. If the Forces are in configuration (a) the solution is $F @ 44.21^{\circ} \nearrow$.

If they are in configuration (b) ( A solution I didn't consider the first time) then $F @ 45.78^{\circ} \searrow$.

 

[rstor]

For configuration (a), if we follow the given diagram, $\phi=45.8°$ and the angle between the initial side and the terminal arm of $\vec A$ is $44.21°$. Is my understanding for this part correct?

 

[erobz]

For configuration (a), if we follow the given diagram, $\phi=45.8°$ and the angle between the initial side and the terminal arm of $\vec A$ is $44.21°$. Is my understanding for this part correct?

Sorry, I didn't realize they had $\phi$ defined off of vertical like that... Yes for figure (a) $\phi=45.8°$

 

[rstor]

Sorry, I didn't realize they had $\phi$ defined off of vertical like that... Yes for figure (a) $\phi=45.8°$

Thank you for confirming. So for figure (b), they have $\phi=45.8°$. As labeled in the diagram, should it not be $\phi=44.2°$.?

 

[erobz]

Thank you for confirming. So for figure (b), they have $\phi=45.8°$. As labeled in the diagram, should it not be $\phi=44.2°$.?

Yeah, as they have it shown in (b) it should be $\phi=44.2°$.

 

[rstor]

Yeah, as they have it shown in (b) it should be $\phi=44.21°$.

Thank you! I thought I had done something wrong.

One thing that is bothering me (from my opening post) is when coming up with the following equation:

$| \vec A |(cos \phi + 2cos111°) = 0$
I could write that $|\vec A|=0$ (by zero product property) and if I substitute this into the other equation I had for the y components I end up with 460 = 0 which is not correct. So I equated the second part $(cos \phi + 2cos111°)$ of the equation to zero and solved for $\phi$. I don't recall coming across a situation when solving simultaneous equations where I could have two possible values to sub into the other equation (with one being invalid). In this case A=0 seems to be invalid. Is there a technical name for this in math? What has happened here?

 

[erobz]

Thank you! I thought I had done something wrong.

One thing that is bothering me (from my opening post) is when coming up with the following equation:

$| \vec A |(cos \phi + 2cos111°) = 0$
I could write that $|\vec A|=0$ (by zero product property) and if I substitute this into the other equation I had for the y components I end up with 460 = 0 which is not correct. So I equated the second part $(cos \phi + 2cos111°)$ of the equation to zero and solved for $\phi$. I don't recall coming across a situation when solving simultaneous equations where I could have two possible values to sub into the other equation (with one being invalid). In this case A=0 seems to be invalid. Is there a technical name for this in math? What has happened here?

I believe they are referred to as Extraneous Solutions.

 

[haruspex]

I believe they are referred to as Extraneous Solutions.

Not sure this counts as an example if an extraneous solution. That term usually refers to where a single equation was manipulated in such a way that the resulting equation had more solutions than the original; e.g. squaring to get rid of a surd.
The example above is not like that. It is perfectly normal for each of a pair of simultaneous equations to have many solutions that do not satisfy the other. Generally, it is an infinite continuum of such. What is special here is that one equation is of the degenerate form xy=0, so only has two solutions.

 

[kuruman]

What has happened here?

Nothing unexpected happened. You correctly came up with the equation
$| \vec A |(cos \phi + 2cos111°) = 0$
As @haruspex remarked, the equation $xy=0$ is degenerate and has two solutions, either $x=0$ or $y=0$. Here, this breaks down to
1. $~cos \phi + 2cos111° = 0$ which leads to the answer as we have seen.

2. $~| \vec A |= 0$. This is mathematically viable, but don't forget that the math in a physics problem describes physical reality. Setting the magnitude of the force $\vec A$ equal to zero automatically sets the magnitude of force $\vec B$ equal to zero because $\vec B=2\vec A.$ This means that the resultant $\vec F_{\text{res}}$ is also zero. The apparent contradiction $460$ N$~=0$ would not have arisen had you used the symbol $|\vec F_{\text{res}}|$ instead of $460~ \text{N}.$ In short, choosing $~| \vec A |= 0$ mathematically describes an alternate reality in which the workers took a lunch break and are no longer pulling on the crate.