- #1
completenoob
- 26
- 0
Homework Statement
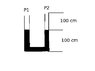
The u-tube shown has a cross-section of 1 cm^2. It contains mercury to the shown levels. The pressure above the the mercury is 750 torr. The left side is sealed off. The right side is is pumped such that the pressure is approximately zero.
i) Determine the far the mercury falls on the left side.
ii) Determine the pressure of the trapped air in the left side.
Temperature is constant
Homework Equations
[tex] P_1-P_2=\Delta h m g[/tex]
[tex] m=\rho V [/tex]
The Attempt at a Solution
i) If there is no air on the right hand side then 100cm of mercury has fallen.
ii)[tex] P_1=\Delta h m g[/tex] where [tex]\Delta h=200[/tex]cm
Is this correct?