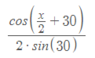The uncertainty is ## \sigma_r ##. They might do well to call it ## \Delta n ##, but they are using statistical type of language, where ## \sigma ## is the letter they use for standard deviation. And yes, what you have is correct. The uncertainty ## \Delta n=\sigma_r=(\frac{dn}{dx})\sigma_L=(\frac{dn}{dx}) \Delta_{\theta_L} ##. ## \\ ## One additional note: This one is a little tricky, because when you put in ## \Delta \theta_L= \sigma_L ## i this formula, you need to convert it to radians, i.e. express ## \Delta \theta_L ## in radians. The result is ## \Delta \theta_L=2 (\frac{\pi}{180} ) ##.Everywhere else you can use degrees, and it doesn't matter, but here you need to have ## \Delta \theta_L ## in radians. ## \\ ## The reason for this is the derivative of the ## \sin(x) ## is equal to the ## \cos(x) ## only when ## x ## is measured in radians. Otherwise there is an additional factor. (This is kind of an advanced topic. I'll try to explain:) To start this explanation, they are basically writing ## dn=\Delta n=(\frac{dn}{d \theta_L}) \, d \theta_L=(\frac{dn}{d \theta_L}) \, \Delta \theta_L ##. The derivative gives you the cosine only if it is measured in radians. The derivative derivation assumes ## \frac{\sin(\Delta x)}{\Delta x }=1 ## for small ## \Delta x ##, but that is only the case of ## \Delta x ## is measured in radians. If ## \Delta x ## is measured in degrees, then in taking the derivative, the factor that appears of ## \frac{\sin(\Delta x)}{\Delta x} ## for small ##\Delta x ## will give a factor of ## \frac{\pi}{180} ## instead of a factor of one.