Understanding Angle Proofs: How to Identify and Solve for Equal Angles

  • Thread starter Thread starter Miike012
  • Start date Start date
  • Tags Tags
    Angle
Click For Summary
SUMMARY

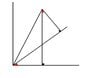
The discussion focuses on understanding angle proofs, specifically how to identify and solve for equal angles in right triangles. The key conclusion is that when two triangles share two angles, the third angles must also be equal due to the properties of triangle congruence. The angles in question are identified as BCA and DCE, which are reflex angles in their respective triangles. This establishes that the red angles in both triangles are equal, confirming the proof of angle equality.

PREREQUISITES
  • Understanding of basic geometric principles, particularly triangle properties.
  • Familiarity with angle relationships, including reflex angles.
  • Knowledge of triangle congruence criteria, such as Angle-Angle (AA) similarity.
  • Ability to interpret geometric diagrams and notations.
NEXT STEPS
  • Study the properties of right triangles and their angle relationships.
  • Learn about triangle congruence criteria, focusing on Angle-Angle (AA) similarity.
  • Explore reflex angles and their significance in geometric proofs.
  • Practice solving angle proofs using various geometric configurations.
USEFUL FOR

Students studying geometry, educators teaching angle proofs, and anyone looking to strengthen their understanding of triangle properties and angle relationships.

Miike012
Messages
1,009
Reaction score
0
Quick angle question...

I am going over the sum of two angles proof... and I am confused about one thing..( my geometry isn't that great) can some one tell me how to two red angles are the same...? thank you.
I posted a pick ...
 

Attachments

  • MATH.JPG
    MATH.JPG
    12.6 KB · Views: 446
Physics news on Phys.org


The two triangles the angles are in are right triangles, right?
At the intersection of the vertical line and the lower of the two slanted lines coming out of the origin, there's one angle of the upper right triangle, and another angle of the lower right triangle. These angles are opposite angles, which means they are equal. So we have two triangles, both with a 90°, and each one has an angle that's equal to an angle in the other triangle. That means that the remaining angles of the two triangles (the ones you're asking about) have to be equal as well.
 


Miike012 said:
I am going over the sum of two angles proof... and I am confused about one thing..( my geometry isn't that great) can some one tell me how to two red angles are the same...? thank you.
I posted a pick ...

Call the lower left vertex A. Let the right angle to the right be B, and the angle above C. Make the red angle above that D and the other right angle E.

Angle BCA is the same as DCE (they are reflex angles). Triangle ABC and DCE are both right angles. That gives two triangles with two angles in common, so the third angles (the red angles) must be equal.

(Sorry about the duplication. In the time I tried to post a lettered diagram, Mark 44 got the answer in.)
 

Similar threads

Finding area of a non right angled triangle
  • · Replies 9 ·
Replies
9
Views
4K
Finding coincident angle between 2 equally spaced sets
  • · Replies 1 ·
Replies
1
Views
2K
Understanding the size of the angle
  • · Replies 4 ·
Replies
4
Views
3K
Angles inscribed in circles part 1
  • · Replies 6 ·
Replies
6
Views
3K
Suggestions for HS geometry book (proofs)
  • · Replies 14 ·
Replies
14
Views
4K
Two roads meeting a river at different angles (heights and distances)
  • · Replies 7 ·
Replies
7
Views
2K
Sum of the angles of a spherical triangle
  • · Replies 1 ·
Replies
1
Views
4K
Bound correlation coefficient for three random variables
  • · Replies 3 ·
Replies
3
Views
4K
How to Determine Correct Inverse Trig Angle?
  • · Replies 2 ·
Replies
2
Views
1K
Angle between a Point on a Ellipse and its Center
  • · Replies 11 ·
Replies
11
Views
3K