Understanding Faddeev-Popov in Schwartz QFT Book

[Lapidus]

In Schwartz QFT book, while explaining the Faddeev-Popov procedure, he presents this following observation at (25.99):

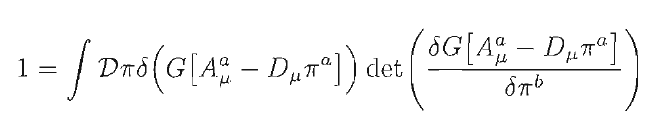
Can someone help understanding me why this expression equals one?

THANK YOU!

 

[Einj]

This is the functional integral extention of the usual relation for a delta functions. Suppose you have an n-dimensional vector field which is a function of another vector, say $\vec v\equiv \vec v(\vec x)$. Then you have:

$$
1=\int d^nv \delta^n(\vec v)=\int d^nx\det\left(\frac{\partial v^i}{\partial x^j}\right) \delta^n(\vec v(\vec x))
$$

It's quite intuitive that the functional integral extension is the one you wrote.