dekoi
Please make your best effort to answer my questions. There are the select few i did not get from two chapters of homework.
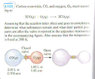
1.) (See attachment).
I'm not quite sure how to work with this question. I assume i must use partial pressures. But don't really understand how to start. I assure you i made an honest attempt to do this question, but really can't figure it out.
2.) A mixture initially consisting of 2 mol CO and 2 mol H2 comes to equilibrium with methanol. At equilibrium, what happens to the amount (in mols; e.g. less than 1 mol, more than 1 mol) of CH3OH?
I assume that there will be less than 1 mol of CH3OH, but can not figure out how to put this into words. Could anyone explain why?
3.) At 850 degrees and 1.0 atm pressure, a gas mixture is in equilibrium is 90.55% CO by mass.
So: C(s) + CO2 (g) <--> 2CO(g)
Calculate Kc.
I assumed 100g of mixture. Therefore, there is 90.55 grams of CO, which can be converted into mols (3.2 mols). By using ratios, i conclude that there is 1.6 C and 1.6 mol of CO2. But this doesn't seem right and does not give me the correct answer.
4.) If i am told that in an equilibrium, the reactant (e.g. 10 mols in 1 L) dissociates to an extent of e.g. 9.5 percent, am i saying that the initial concentration is 10, and that the equilibrium concentration of that reactant is 10 - 0.095*10 ?
Thank you very much.
1.) (See attachment).
I'm not quite sure how to work with this question. I assume i must use partial pressures. But don't really understand how to start. I assure you i made an honest attempt to do this question, but really can't figure it out.
2.) A mixture initially consisting of 2 mol CO and 2 mol H2 comes to equilibrium with methanol. At equilibrium, what happens to the amount (in mols; e.g. less than 1 mol, more than 1 mol) of CH3OH?
I assume that there will be less than 1 mol of CH3OH, but can not figure out how to put this into words. Could anyone explain why?
3.) At 850 degrees and 1.0 atm pressure, a gas mixture is in equilibrium is 90.55% CO by mass.
So: C(s) + CO2 (g) <--> 2CO(g)
Calculate Kc.
I assumed 100g of mixture. Therefore, there is 90.55 grams of CO, which can be converted into mols (3.2 mols). By using ratios, i conclude that there is 1.6 C and 1.6 mol of CO2. But this doesn't seem right and does not give me the correct answer.
4.) If i am told that in an equilibrium, the reactant (e.g. 10 mols in 1 L) dissociates to an extent of e.g. 9.5 percent, am i saying that the initial concentration is 10, and that the equilibrium concentration of that reactant is 10 - 0.095*10 ?
Thank you very much.