Phoenixtears
- 82
- 0
GREEN= Correct
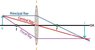
The lens in the figure is used to produce a real image of a candle flame at the 36 cm mark. What is the focal length of the lens?
focal length= 9
(My attachments aren't working, however, if you were to draw a line, put a lens in the middle, then a small candle on the left and a magnified, inverted candle on the left, that's the drawing. The length from the object from the small candle to the lens is 12cm at first, and the length from the lens to the larger image of the candle is 36 at first, the changed lengths are mentioned below. I'm so sorry about this).
Change the location of the object to 11 cm. Determine the location and magnification of the image.
location= 49.5
magnification=____
h'/h= s'/s= magnification
In other words: the ratio of height of object to height of image equals the ratio of length to lens for the object to the length to lens of the image, which equals magnification.
I don't understand why the magnification problem isn't panning out. I'm using the equation above, stating that the image distance over the object distance equals the magnification. So, with the new numbers, it would look like this:
49.5/11= 4.5
However, this isn't the answer. Can anyone help me out with this one?
Thanks in advance!
~Phoenix
Homework Statement
The lens in the figure is used to produce a real image of a candle flame at the 36 cm mark. What is the focal length of the lens?
focal length= 9
(My attachments aren't working, however, if you were to draw a line, put a lens in the middle, then a small candle on the left and a magnified, inverted candle on the left, that's the drawing. The length from the object from the small candle to the lens is 12cm at first, and the length from the lens to the larger image of the candle is 36 at first, the changed lengths are mentioned below. I'm so sorry about this).
Change the location of the object to 11 cm. Determine the location and magnification of the image.
location= 49.5
magnification=____
Homework Equations
h'/h= s'/s= magnification
In other words: the ratio of height of object to height of image equals the ratio of length to lens for the object to the length to lens of the image, which equals magnification.
The Attempt at a Solution
I don't understand why the magnification problem isn't panning out. I'm using the equation above, stating that the image distance over the object distance equals the magnification. So, with the new numbers, it would look like this:
49.5/11= 4.5
However, this isn't the answer. Can anyone help me out with this one?
Thanks in advance!
~Phoenix
Attachments
Last edited: