Understanding the Bouncing and Rolling Motion of a Cube (Die) on a Slope

[Mins]

How a cube(a die) rolls(rolling motion help)

I want to show how a cube bounces and rolls when dropped from a slope(45 degrees).

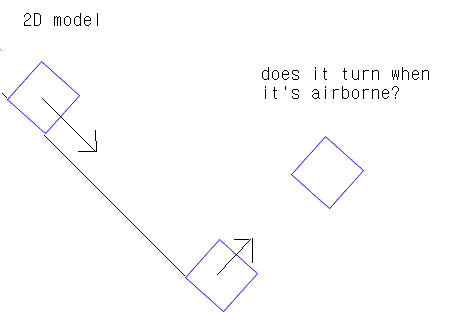
I'm trying to make this problem as easy as possible, so I've ruled out air current.
How will it bounce? Think I need to use 'e'(elasticity)(which is roughly 0.3)...
Then, I don't understand why it rolls when it's airborne... Does it roll at all? Did I miss something?

Another thing that bothers me is it's rolling motion when it's not bouncing up and down...

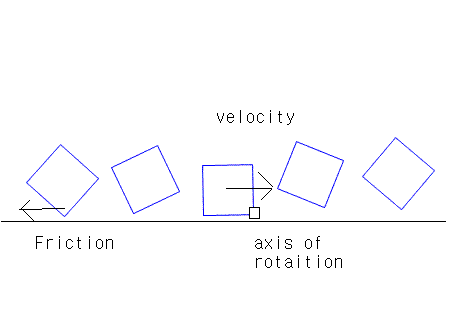(Not sure of it and don't know what determines rolling friction)
Where does the axis of the die lie?
and what is conserved, and what isn't?

extra)http://director-online.com/buildArticle.php?id=1075#dice

 

[Astronuc]

Die are three dimensional objects. The interaction with a surface is asymmetric (striking a surface on one corner, edge or face), and the force acting in opposition to forward motion acts at a distance to its center of mass, which produces a 'moment' about the center of mass, and hence the development of rotational motion.

The collision is largely elastic since there is little deformation of the surface or die.

 

[Mins]

I think I understand but

the force acting in opposition to forward motion acts at a distance to its center of mass, which produces a 'moment' about the center of mass, and hence the development of rotational motion.
QUOTE]

I'm sorry if I'm asking too much, but can you make a formula out of this?

 

[Mins]

...

or suggest a formula to calculate?