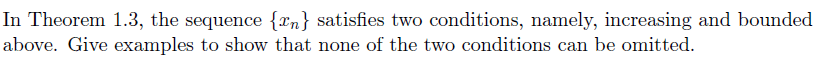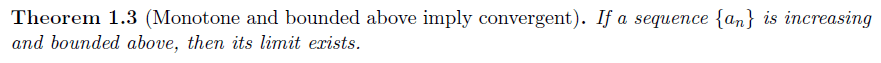Understanding the Cauchy-Schwarz Inequality

Click For Summary
SUMMARY

The discussion centers on the Cauchy-Schwarz Inequality, emphasizing the necessity of both conditions: an increasing sequence and boundedness. Participants highlight the need for specific examples to illustrate divergent sequences that meet these criteria. The two required examples are: (i) a divergent sequence that is increasing but not bounded above, and (ii) a divergent sequence that is bounded above but not increasing. These examples are crucial for demonstrating the theorem's validity.

PREREQUISITES
  • Understanding of the Cauchy-Schwarz Inequality
  • Familiarity with divergent sequences in mathematics
  • Knowledge of bounded and unbounded sequences
  • Basic concepts of mathematical proofs
NEXT STEPS
  • Research examples of divergent sequences in real analysis
  • Study the implications of the Cauchy-Schwarz Inequality in vector spaces
  • Explore the relationship between increasing sequences and convergence
  • Learn about bounded versus unbounded sequences in mathematical contexts
USEFUL FOR

Mathematicians, students studying real analysis, educators teaching inequalities, and anyone interested in the applications of the Cauchy-Schwarz Inequality.

Joe20
Messages
53
Reaction score
1
I am not sure what examples to give, need help on this. Have attached the theorem as well.
 

Attachments

  • Untitled.png
    Untitled.png
    5.9 KB · Views: 110
  • 11111.png
    11111.png
    6.4 KB · Views: 116
Physics news on Phys.org
You need to give an example of (i) a divergent sequence that is increasing but not bounded above, and (ii) a divergent sequence that is bounded above but not increasing. This will show that both conditions (increasing and bounded) are needed for the theorem to hold.
 

Similar threads

MHB Cauchy-Schwarz Inequality - Duistermaat and Kolk, CH. 1, page 4 .... ....
  • · Replies 1 ·
Replies
1
Views
2K
Graduate How can I Prove the following Integral Inequality?
  • · Replies 2 ·
Replies
2
Views
2K
Undergrad Schwarz inequality is Cauchy–Schwarz inequality?
  • · Replies 5 ·
Replies
5
Views
5K
MHB Lagrange's Identity and Cauhchy-Schwarz Inequality for complex numbers
  • · Replies 1 ·
Replies
1
Views
7K
MHB How does Remmert derive the Cauchy-Schwarz Inequality in complex functions?
  • · Replies 4 ·
Replies
4
Views
2K
MHB Normed and Inner Product Spaces .... Garling, Corollary 11.3.2 ....
  • · Replies 2 ·
Replies
2
Views
1K
MHB Law of Cosines for C .... Remmert Section 1.3, Ch. 0 ....
  • · Replies 1 ·
Replies
1
Views
1K
MHB How is this inequality obtained?
  • · Replies 5 ·
Replies
5
Views
2K
MHB Absolute Value of Complex Integral
  • · Replies 1 ·
Replies
1
Views
2K
Graduate Cauchy schwarz inequality in Rudin
  • · Replies 1 ·
Replies
1
Views
4K