Understanding the concepts of capacitors

[recomendacion]

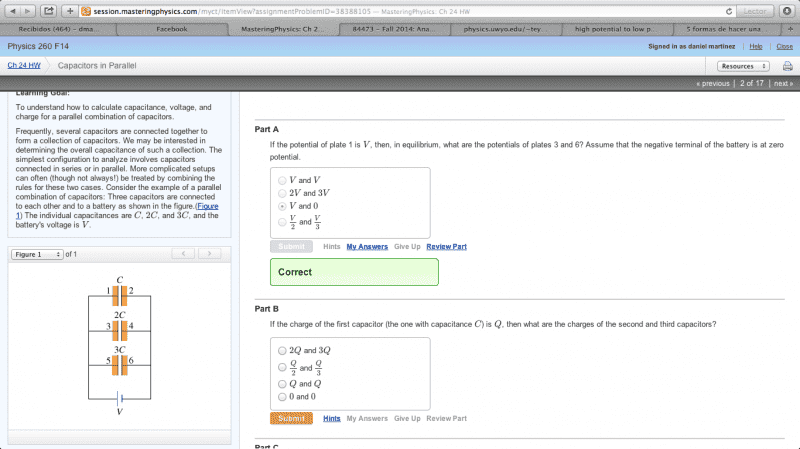
I feel so frustrated because I could not understand the basics of this topic. My teacher spent like 1 week trying to explain it. I understood the math of capacitors, but I could not understand what an electric potential is. For example, what do you really mean? when you have a capacitor and apply it an electrical potential??. Here you have conceptual questions. Help me please

 

[CWatters]

For example, what do you really mean? when you have a capacitor and apply it an electrical potential??.

Basically it means you are charging up the capacitor by connecting it to a voltage source. That will put electrons on one plate so that there is a matching voltage difference (electric potential) between the two plates.