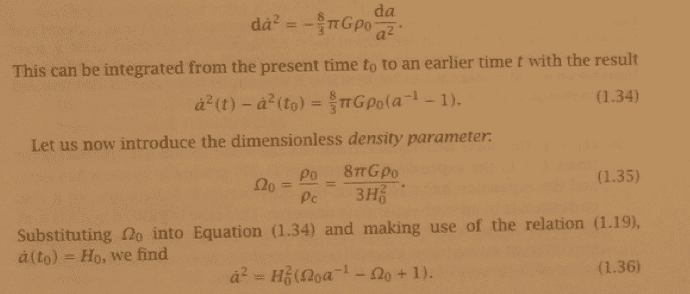Understanding the Density Parameter in Cosmology: Matts Roos' Text Explanation

[robertjford80]

This is from Matts Roos' text on cosmology. I don't follow the final step and when he integrates I understand the first part of the left side, and the right side. But I don't see where -a'^2(t₀) comes from

 

[twofish-quant]

It's a constant of integration. Since you can add an arbitrary constant and have the differential equation still work, instead of writing C, he writes the constant so that the numbers end up nice later.

 

[phyzguy]

Or you can view it as a definite integral with limits:
$$\int^t_{t_0}d(\dot a^2) = -{H_0}^2 \Omega_0\int^t_{t_0}\frac{da}{a^2}$$

$$\dot a^2(t) - \dot a^2(t_0)={H_0}^2 \Omega_0(\frac{1}{a(t)}-\frac{1}{a(t_0)})$$
$$\dot a^2(t) - {H_0}^2={H_0}^2 \Omega_0(\frac{1}{a(t)}-1)$$
$$\dot a^2(t) ={H_0}^2( \frac{\Omega_0}{a(t)}-\Omega_0+1)$$

Note that we define the current scale parameter a(t0) to be 1, and since the Hubble constant H is defined to be adot/a, that H(t0) = adot(t0)/a(t0) = adot(t0), since a(t0)=1.

 

[robertjford80]

i still don't understand the progression from 1.35 to 1.36

 

[phyzguy]

i still don't understand the progression from 1.35 to 1.36

I edited my earlier post to add more detail. Does this clear it up?

 

[robertjford80]

i'm falling asleep so i'll look at it tomorrow

 

[cepheid]

i still don't understand the progression from 1.35 to 1.36

The progression from 1.35 to 1.36 is just algebra. Notice that if you take the leftmost side of 1.35, and the rightmost side of it, and you multiply them both by H₀², then you end up with$$\Omega_0 H_0^2 = \frac{8\pi G}{3}\rho_0$$So, anywhere that you see $8\pi G \rho_0 / 3$ in 1.34, just replace it with $\Omega_0 H_0^2$.

 

[robertjford80]

The progression from 1.35 to 1.36 is just algebra. Notice that if you take the leftmost side of 1.35, and the rightmost side of it, and you multiply them both by H₀², then you end up with$$\Omega_0 H_0^2 = \frac{8\pi G}{3}\rho_0$$So, anywhere that you see $8\pi G \rho_0 / 3$ in 1.34, just replace it with $\Omega_0 H_0^2$.

If omega H²₀ = 8piGrho/3 then I don't see where the final +1 comes from in equation 1.36

 

[cepheid]

If omega H²₀ = 8piGrho/3 then I don't see where the final +1 comes from in equation 1.36

It comes from the very constant of integration that you were asking about before!

making use of the relation (1.19), $\dot{a}(t_0) = H_0$, we find

 

[robertjford80]

ok, thanks