Understanding the Equation of Motion for Simple Harmonic Motion

[ZARATHUSTRA]

For one-dimensional simple harmonic motion, the equation of motion, which is a second-order linear ordinary differential equation with constant coefficients, could be obtained by means of Newton's second law and Hooke's law

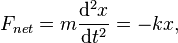and

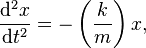i don't get this part

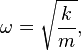which [PLAIN]http://upload.wikimedia.org/math/6/5/6/656fd81e91b7ad38db0c1f263dd5f4af.png[/B]

so can somebody explain it to me? Thank you

 

[vela]

What don't you get?

 

[RUber]

The first part is the solution to the differential equation.
The second part is a recast of the solution with one function (cosine).
If you let $\frac{c_2}{c_1}=\tan \phi$ this is the angle sum identity for cosine.

 

[ZARATHUSTRA]

why? why "w'' = the square root of 'k' divided by 'm' i don't get this equation

 

[vela]

Try plugging $x(t) = A\cos(\omega t-\varphi)$ into the differential equation.

 

[ZARATHUSTRA]

Try plugging $x(t) = A\cos(\omega t-\varphi)$ into the differential equation.

how do they people get this equation?

, where does it come from? can you show me process of deducting this formula? THANKS!

 

[vela]

Did you try plugging x(t) into the differential equation?

 

[RUber]

It is simply a notational convenience. You could continue to use sqrt(k/m) everywhere but that gets messy.