Understanding the Meaning of "Proper Time"

[Zephaniah]

What is proper time? How can I solve proper time? "There is only one frame of reference in which clock is at rest, and there are infinitely many in which it is moving." What does it mean?

 

[haushofer]

If you take 2 events, you can define the elapsed time between them in different ways, and this will give you different answers in general. That's the idea of relativity. One way to define the time between these events, is to use a clock of an observer which travels between these 2 events. The time elapsed on its clock is what we call the proper time. I think this also refers to your quote, but if you give quotes, it is common here to say where you get it from.

I'm not sure what you mean by "solving proper time", though.

 

[Dale]

What is proper time? How can I solve proper time?

Given some time like worldline, proper time is the time measured by a clock traveling along that worldline. It is given by $\tau=\int_P \sqrt{1-v^2/c^2}dt$

 

[Ibix]

Proper time is the time measured by some chosen clock - e.g. your watch - traveling between two events.

If it is possible to get from one event to the other without exceeding the speed of light then the proper time of a clock moving inertially between the events is the same as the coordinate time between the events in a frame where that clock is at rest.

Dale gave the correct formula to calculate the proper time between two events along some path. However, do note that in the case where the clock is moving inertially, v is not a function of t and the integral is trivial.

 

[Chestermiller]

I think what you are asking is, "Is it possible for observers that are traveling in frames of reference that are not at rest with respect to the specified clock to determine, exclusively from measurements in their own frame of reference, what the change in proper time is on the subject clock?" The answer is yes.

 

[pervect]

To measure proper time, you need a clock. You start the clock at some event, and you stop the clock at some other event. The reading of the clock is the proper time.

Proper time is the simplest sort of time. There are more complicated notions of time. I am guessing that your notion of "time" includes some notion of "now". The notion of now requires some mechanism to tell when two events at different locations in space occur "at the same time", this is usually called "synchronization".

Proper time, being the simplest sort of time, doesn't require any notion of "now". It only requires clocks - stopwatches, basically.

If you want to know more about other notions of time and how they relate to proper time, ask. But I think the above explanation of proper time is sufficient to answer what you asked, though it may or may not tell you what you wanted to know. If it's not sufficient, perhaps asking more questions would clarify what you needed.

 

[Zephaniah]

Thank you for the explanations up there. For everyone's information, I am a college student and this topic "Proper Time" is my report. And I am really having a hard time how to understand this concept that is why I still don't have a concrete idea about this one.

 

[Zephaniah]

Now, I understand that Proper time is what the observer's clock reads. Right? How about if there are 2 observers with their own clock at the same event but they come up with a conclusion that the event happen with a different time in there clock which one will I consider as proper time?

 

[Chestermiller]

Thank you for the explanations up there. For everyone's information, I am a college student and this topic "Proper Time" is my report. And I am really having a hard time how to understand this concept that is why I still don't have a concrete idea about this one.

The questions you asked in your initial post were very general. Maybe it would help if you asked more specific questions. Is this your only discomfort with the basics of special relativity? Or are other aspects of special relativity limiting your ability to understand property time.

 

[Zephaniah]

If you take 2 events, you can define the elapsed time between them in different ways, and this will give you different answers in general. That's the idea of relativity. Does it mean that each observer is correct whatever they state of what they have observed?

 

[Zephaniah]

The questions you asked in your initial post were very general. Maybe it would help if you asked more specific questions. Is this your only discomfort with the basics of special relativity? Or are other aspects of special relativity limiting your ability to understand property time.

My teacher told me that there is a computation for proper time and I as I browse in the internet the formulas are confusing. I think I need a step by step instruction to solve it.

 

[Chestermiller]

Now, I understand that Proper time is what the observer's clock reads. Right? How about if there are 2 observers with their own clock at the same event but they come up with a conclusion that the event happen with a different time in there clock which one will I consider as proper time?

If the two observers are at rest relative to one another (and, thus, they are both physically present at both events) their clocks will both show the same elapsed proper time. If the two observers are in relative motion, then they can't both be physically present at both of the two events.

 

[Chestermiller]

My teacher told me that there is a computation for proper time and I as I browse in the internet the formulas are confusing. I think I need a step by step instruction to solve it.

Dale gave the equation in post #3. Is this the equation you are finding complicated to solve? Which part are you finding complicated?

 

[Zephaniah]

If the two observers are at rest relative to one another (and, thus, they are both physically present at both events) their clocks will both show the same elapsed proper time. If the two observers are in relative motion, then they can't both be physically present at both of the two events.

Is it the same with inertial reference and relativity of simultaineity?

 

[Chestermiller]

Is it the same with inertial reference and relativity of simultaineity?

Sorry, I have no idea what you are asking here. It seems to me your problems are much broader than just not understanding proper time.

 

[Zephaniah]

Dale gave the equation in post #3. Is this the equation you are finding complicated to solve? Which part are you finding complicated?

Yes Sir. That formula is too complicated for me.

 

[Chestermiller]

Yes Sir. That formula is too complicated for me.

In what way? Have you not had integral calculus?

 

[Zephaniah]

Sorry, I have no idea what you are asking here. It seems to me your problems are much broader than just not understanding proper time.

My problem is how am I going to teach the concept of proper time to my classmates and how am I going to show some problem solving to them.

 

[Zephaniah]

In what way? Have you not had integral calculus?

Yes Sir. I haven't learn integral calculus yet.

 

[Chestermiller]

My problem is how am I going to teach the concept of proper time to my classmates and how am I going to show some problem solving to them.

Let's see your attempt to do this so far. What is your best shot at explaining this?

 

[Zephaniah]

Let's see your attempt to do this so far. What is your best shot at explaining this?

Maybe I'll draw an illustration showing an observer inside the event and another observer outside the event. Then I'll ask them if who among the two know the proper time. Then the answer will be both have observed the event at a different time but both of them has the proper time in their own reference.

 

[Ibix]

Concepts you may find helpful:
- Interval $\Delta s^2=c^2\Delta t^2-(\Delta x^2+\Delta y^2 +\Delta z^2)$
- Worldlines
- Block universe
- Events
- Minkowski diagram

The block universe is 4d spacetime. Events are points in space at a given time. Worldlines are lines joining events - your worldline joins all the events you passed through in your life. Interval is the generalisation of Pythagorean distance to spacetime. You may wish to look up the relationship between proper time and interval, and then think about what a worldline's proper time means.

Note also that "proper" in this context is being used in its original Latin sense of "one's own", rather like "property". Not in the modern English sense of "correct".

 

[Chestermiller]

Yes Sir. I haven't learn integral calculus yet.

If you confine attention to inertial frames of reference that are in relative motion with respect to one another with velocity v, then the equation simplifies to $\Delta \tau=\sqrt{1-\left(\frac{v}{c}\right)^2}\Delta t$. Imagine that you have a single observer with a clock that is at rest in his frame of reference, and measures the time interval between the two events $\Delta \tau$ (he is physically present at both events). Imagine that this observer is moving with velocity v relative to a (stationary) group of observers strung out along the route from the first event to the second event, and the two observers physically present at the two events write down the times on their synchronized clocks at which the two events occur. They then get together and compare notes, and, when they do, they find that, according to their clocks, the time interval between the two events is $\Delta t$. The equation above will tell you the relationship between $\Delta \tau$ and $\Delta t$ (which will not be the same).

 

[Chestermiller]

Maybe I'll draw an illustration showing an observer inside the event and another observer outside the event. Then I'll ask them if who among the two know the proper time. Then the answer will be both have observed the event at a different time but both of them has the proper time in their own reference.

Only the observer who is at rest and personally observes the two events can be physically present at both of the events. The other observer you are referring to (in a different frame of reference) can be physically present at either of the events, but not both of them.

 

[Zephaniah]

If you confine attention to inertial frames of reference that are in relative motion with respect to one another with velocity v, then the equation simplifies to $\Delta \tau=\sqrt{1-\left(\frac{v}{c}\right)^2}\Delta t$. Imagine that you have a single observer with a clock that is at rest in his frame of reference, and measures the time interval between the two events $\Delta \tau$. Imagine that this observer is moving with velocity v relative to a (stationary) group of observers strung out along the route from the first event to the second event, and the two observers physically present at the two events write down the times on their synchronized clocks at which the two events occur. They then get together and compare notes, and, when they do, they find that, according to their clocks, the time interval between the two events is $\Delta t$. The equation above will tell you the relationship between $\Delta \tau$ and $\Delta t$ (which will not be the same).

This one formula is much easier than before but I think I need to try this one first. May I ask if you have any problem solving for me to solve?

 

[Zephaniah]

Only the observer who is at rest and personally observes the two events can be physically present at both of the events. The other observer you are referring to (in a different frame of reference) can be physically present at either of the events, but not both of them.

What if they both see the event? I mean the other one is present at the event (lets call it observer 1) and the other one just saw the event (observer 2). Observer 1 says that the event happen at 7:00 am while observer 2 says that it occur at 7:05 am. Then where is the proper time?

 

[Chestermiller]

This one formula is much easier than before but I think I need to try this one first. May I ask if you have any problem solving for me to solve?

OK. The single observer with the clock is traveling at 0.9c relative to the stationary group of observers (strung out along the route) with their clocks. The single observer who is physically present at the two events notes that the time interval between these two events is 1 hour. Now, for the group of observers strung out along the route with their clocks, when they get together and compare notes, what do they measure the time interval between the same two events to be?

 

[Chestermiller]

What if they both see the event? I mean the other one is present at the event (lets call it observer 1) and the other one just saw the event (observer 2). Observer 1 says that the event happen at 7:00 am while observer 2 says that it occur at 7:05 am. Then where is the proper time?

You can't just talk about one event. You need to talk about the time interval between two events. The actual times on their clocks don't matter. Only the time interval between the events matter. That's what we mean by proper time.

 

[Chestermiller]

I need to go off-line now. Maybe other members can continue this discussion with you.

 

[Zephaniah]

Concepts you may find helpful:
- Interval $\Delta s^2=c^2\Delta t^2-(\Delta x^2+\Delta y^2 +\Delta z^2)$
- Worldlines
- Block universe
- Events
- Minkowski diagram

The block universe is 4d spacetime. Events are points in space at a given time. Worldlines are lines joining events - your worldline joins all the events you passed through in your life. Interval is the generalisation of Pythagorean distance to spacetime. You may wish to look up the relationship between proper time and interval, and then think about what a worldline's proper time means.

Note also that "proper" in this context is being used in its original Latin sense of "one's own", rather like "property". Not in the modern English sense of "correct".

I think I will not search about the worldline anymo

OK. The single observer with the clock is traveling at 0.9c relative to the stationary group of observers (strung out along the route) with their clocks. The single observer who is physically present at the two events notes that the time interval between these two events is 1 hour. Now, for the group of observers strung out along the route with their clocks, when they get together and compare notes, what do they measure the time interval between the same two events to be?

I can't solve this one. I don't know the value of change in time/delta t or whatever it is called.

 

[Zephaniah]

You can't just talk about one event. You need to talk about the time interval between two events. The actual times on their clocks don't matter. Only the time interval between the events matter. That's what we mean by proper time.

I'm still confused. I'm so sorry. My brain just can't absorb these informations. :(

 

[Zephaniah]

I need to go off-line now. Maybe other members can continue this discussion with you.

Thank you Sir. I hope I can understand all of these later.

 

[robphy]

Given some time like worldline, proper time is the time measured by a clock traveling along that worldline. It is given by $\tau=\int_P \sqrt{1-v^2/c^2}dt$

This might help the OP...
This is an annotated spacetime diagram (a position-vs-time diagram, with time running upwards (by convention)).
Note that we are using the geometry of Minkowski spacetime--not Euclidean geometry (and not the Galilean geometry of the PHY101 position-vs-time graph).

The segment OP is a portion of Alice's worldline (who is at rest in this diagram).
The segment OQ is a portion of Bob's worldline (who is moving with velocity v in this diagram).
According to Alice, events (akin to 'points') P and Q are simultaneous (which is geometrically interpreted by saying that PQ is Minkowski-perpendicular to OP).

It is useful to think in terms of "rapidity" $\theta$ (the Minkowski-angle between two inertial observers).
We have Bob's velocity [according to Alice] as $v=c\tanh\theta$.

For an inertial path OQ through spacetime (the inertial 'worldline' OQ ),
the proper time along that worldline (akin to an arc length along a path) is $\tau_{OQ}$.
Observe that OQ is the hypotenuse of a MInkowski-right triangle.
The adjacent side OP is related by $\tau_{OP}=\left( \cosh\theta\right) \tau_{OQ}$.
So,
$$\begin{eqnarray*}
\tau_{OQ}
&=&\left( \frac{1}{\cosh\theta}\right) \tau_{OP}\\
&=&\left( \sqrt{1-\tanh^2\theta}\right) \tau_{OP}\\
&=&\left( \sqrt{1-(v/c)^2}\right) \tau_{OP}.\\
&=&\left( \sqrt{1-(v/c)^2}\right) t.\\
\end{eqnarray*}$$
The last form is for describing the worldline as a 'function of t'.

If the path of interest is more complicated, the formula is generalized.
For piecewise inertial, add up the separate pieces, $$\tau=\sum_i \sqrt{1-(v_i/c)^2}\Delta t_i.$$
More generally, $$\tau=\int \sqrt{1-(v/c)^2}\ dt.$$
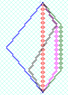
Here's an example of the ClockEffect/TwinParadox.
Suppose that are three worldlines from O to Z,
one inertial,
one with there-and-back speeds of (6/10)c,
and the last has there-and-back speeds of (8/10)c.

The inertial worldline OZ (with velocity 0 in this frame) has proper time 20.
$$\tau_{OPZ}=\sqrt{1-0^2}(20)=20.$$
The piecewise-inertial worldline OQZ has proper time 16.
$$\tau_{OQZ}=\tau_{OQ}+\tau_{QZ}=\sqrt{1-(6/10)^2}(10)+\sqrt{1-(-6/10)^2}(10)=8+8=16.$$
The piecewise-inertial worldline ORZ has proper time 12.
$$\tau_{ORZ}=\tau_{OR}+\tau_{RZ}=\sqrt{1-(8/10)^2}(10)+\sqrt{1-(-8/10)^2}(10)=6+6=12.$$

To visualize this, it is useful to draw a spacetime diagram on rotated graph paper (so that ticks are easier to draw).

Here's a more elaborate example.
I'll leave it to you to work out the numbers.

(See my insights for more information:
https://www.physicsforums.com/insights/spacetime-diagrams-light-clocks/
https://www.physicsforums.com/insights/relativity-rotated-graph-paper/ )

 

[Pencilvester]

You can't just talk about one event. You need to talk about the time interval between two events. The actual times on their clocks don't matter. Only the time interval between the events matter. That's what we mean by proper time.

I'm still confused. I'm so sorry. My brain just can't absorb these informations. :(

The time that you happen to set your watch to is not physically significant. If you are looking at a situation in which there are two observers and a single event, in the absence of additional information about the scenario, the only meaningful (although trivial) statement you can make is that both observers agree that the event occurred. Saying what time each observer determines the event to have happened is arbitrary, as you can set your watch to whatever time you like. More interesting situations compare what two different observers determine the elapsed time to be between two distinct events because that does not depend on what time you set your watch to.

If the two observers are in motion relative to one another, then generally the elapsed coordinate time that each observer measures between the events will differ. However, if there is an object that is present at both events (there doesn’t have to be a physical object, but it makes the scenario more concrete), and if each observer works out the elapsed proper time of the object’s path through spacetime (its worldline) between the two events, then they will both get the same result. If the object happens to be a clock, then the elapsed time that that clock measures is the same as the proper time.

 

[Dale]

Yes Sir. That formula is too complicated for me.

I have changed the level of the thread to B to help respondents answer at the appropriate level of complication. To make this feasible to answer at this level, I will consider only inertial coordinates in flat spacetime with a single dimension of space.

Then the proper time between two events is $\Delta \tau = \sqrt{\Delta t^2-\Delta x^2/c^2}$ where $\Delta t$ is the difference in coordinate time and $\Delta x$ is the difference in coordinate position between the two events and $\Delta \tau$ is the proper time, or the time measured by a clock that travels inertially from one event to the other.