Understanding the Motion of a Bead on a Rotating Rod

[Saitama]

Homework Statement

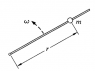
A bead of mass m slides without friction on a rod that is made to rotate at a constant angular velocity $\omega$. Neglect gravity.

a. Show that $r=r_0e^{\omega t}$ is a possible motion of the bead, where $r_0$ is the initial distance of the bead from the pivot.

b. For the motion described in part a, find the force exerted on the bead by the rod.

c. For the motion described above, find the power exerted by the agency which is turning the rod and show by direct calculation that this power equals the rate of change of kinetic energy of the bead.

Homework Equations

The Attempt at a Solution

In the frame fixed to the rotating rod, the force acting on the bead is radially outwards and is of magnitude $m\omega^2r$. Hence,
$$m\frac{d^2r}{dt^2}=m\omega^2r$$
The solution to the above equation is:
$$r(t)=Ae^{\omega t}+Be^{-\omega t}$$
The motion presented in the question is possible when $r(0)=r_0$ and $r'(0)=r_0$. Is this correct?

How do I solve the b part? What is the direction of force acting on the bead by the rod?

The bead has both tangential $(a_t)$ and radial $(a_r)$ acceleration.
$$a_t=\frac{dv_t}{dt}$$
where $v_t$ is the tangential velocity. Since $v_t=\omega r=\omega r_0e^{\omega t}$,
$$a_t=\omega^2r_0e^{\omega t}$$
Also $a_r=\omega^2r=\omega^2r_0e^{\omega t}$.

Net acceleration: $\sqrt{a_t^2+a_r^2}$. Hence, force due to rod is $F=m\sqrt{a_t^2+a_r^2}$. Is this correct?

Any help is appreciated. Thanks!

 

[voko]

The rod cannot exert any radial force on the bead, there is no friction.

 

[Saitama]

The rod cannot exert any radial force on the bead, there is no friction.

Okay, so that means the force on the bead is $ma_t$. Right?

I am confused by my attempt, which force provides the radial acceleration then?

 

[voko]

The radial acceleration is an artifact of the non-inertial frame.

Keep in mind that at any given moment the bead "wants" to travel tangentially. A moment later the tangential direction is different, and the difference has a radial component, so in the co-moving frame that looks like a result of radial acceleration.

The description above is simplified because at the "given moment" there is also non-zero radial velocity.

 

[Chestermiller]

This problem is easier to do using vectors. Let $\vec{r}=r(t)\vec{i_r}(t)$. From this, the bead velocity is
$$\vec{v}=\frac{d\vec{r}}{dt}=\frac{dr}{dt}\vec{i_r}+r\frac{d\theta}{dt} \vec{i_θ}$$
Taking the derivative again to get the acceleration:
$$\vec{a}=\frac{d\vec{v}}{dt}=\left(\frac{d^2r}{dt^2}-r\left(\frac{dθ}{dt}\right)^2\right)\vec{i_r}+2\frac{dr}{dt}\frac{dθ}{dt} \vec{i_θ}=\left(\frac{d^2r}{dt^2}-r\omega^2\right)\vec{i_r}+2\omega\frac{dr}{dt}\vec{i_θ}$$
The radial acceleration is zero, and the tangential accleration is $2\omega\frac{dr}{dt}$. This is what they sometimes call the Coriolis acceleration.

 

[Saitama]

The radial acceleration is an artifact of the non-inertial frame.

Keep in mind that at any given moment the bead "wants" to travel tangentially. A moment later the tangential direction is different, and the difference has a radial component, so in the co-moving frame that looks like a result of radial acceleration.

The description above is simplified because at the "given moment" there is also non-zero radial velocity.

Understood. Thank you very much. :)

How to approach the c part? Do I have to use that power is $\vec{\tau}\cdot\vec{\omega}$?

The force acting on the rod is $ma_t=m\omega^2r_0e^{\omega t}$. The torque due to this force is $m\omega^2r_0^2e^{2\omega t}$. Hence the power supplied by the external agency is:

$$m\omega^3r_0^2e^{2\omega t}$$

The kinetic energy of the bead at any instant is:
$$K=\frac{1}{2}m(v_t^2+v_r^2)=\frac{1}{2}m(\omega^2r_0^2e^{2\omega t}+\omega^2r_0^2e^{2\omega t})$$
$$\Rightarrow K=m\omega^2r_0^2e^{2\omega t}$$
where $v_r$ is the radial velocity and can be calculated by $dr/dt$.
The rate of change of kinetic energy is
$$\frac{dK}{dt}=2m\omega^3r_0^2e^{2\omega t}$$
But this doesn't matches with power I calculated before. Where did I go wrong?

 

[voko]

You did not compute the tangential acceleration properly. You differentiated the tangential speed, but that is not tangential acceleration, so you are off by a factor of $2 \omega$. Look at the correct derivation by Chestermiller.

 

[Saitama]

You did not compute the tangential acceleration properly. You differentiated the tangential speed, but that is not tangential acceleration, so you are off by a factor of $2 \omega$. Look at the correct derivation by Chestermiller.

I had a look at Chestermiller's post but it looks to me that Chestermiller has used polar coordinates and I don't want to get in that mess.

Is there no other way? If there is not, I will see about polar coordinates.

 

[voko]

Is there no other way? If there is not, I will see about polar coordinates.

Chestermiller used the tangential/radial decomposition just like you did. It is equivalent to using polar coordinates in this case. He did all the hard work, anyway, so I do not see why you should shy away from that.

 

[Chestermiller]

You did not compute the tangential acceleration properly. You differentiated the tangential speed, but that is not tangential acceleration, so you are off by a factor of $2 \omega$. Look at the correct derivation by Chestermiller.

Actually, he's only off by a factor of 2 on the tangential acceleration. That's why he got the correct answer for the power using the KE approach, but only half the correct answer when he calculated the power from the torque.

Chet

 

[Chestermiller]

Hi Pranav-Arora,

The big question is "why did your analysis only give half the correct value for the circumferential acceleration?" Here is a hint: You need to consider the rate of change of the radial velocity component.

Chet

 

[Saitama]

The big question is "why did your analysis only give half the correct value for the circumferential acceleration?" Here is a hint: You need to consider the rate of change of the radial velocity component.

I don't get this. As per the part b of the problem, the force on the bead is in the tangential direction. Hence, an equal and opposite force acts on the rod. The agency must supply the power against the torque due to this force to keep the rod rotating at a constant angular velocity. So in the formula of power i.e $\tau \cdot \omega$, I should plug in this value of torque. Where is this incorrect? How does the radial component comes in the picture?

Or is my expression for tangential acceleration incorrect? To be sure, the answer to part b is $ma_t$, right?

 

[voko]

Or is my expression for tangential acceleration incorrect? To be sure, the answer to part b is $ma_t$, right?

Your result for the tangential acceleration is incorrect by the factor of 2, as Chestermiller pointed out. He gave the correct derivation in #5. Your derivation in #1 is incorrect, because you took the tangential speed and differentiated it with respect to time; but tangential acceleration does not just change the speed, it changes the direction of velocity, too, so that must be taken into account. Again, look at #5, the answer is there.

 

[Chestermiller]

I don't get this. As per the part b of the problem, the force on the bead is in the tangential direction. Hence, an equal and opposite force acts on the rod. The agency must supply the power against the torque due to this force to keep the rod rotating at a constant angular velocity. So in the formula of power i.e $\tau \cdot \omega$, I should plug in this value of torque. Where is this incorrect? How does the radial component comes in the picture?

Or is my expression for tangential acceleration incorrect? To be sure, the answer to part b is $ma_t$, right?

Part of the problem is calling it the tangential acceleration. You should be calling it the circumferential acceleration. Here's how the radial component of velocity comes into the picture when calculating the circumferential acceleration. Don't forget that the acceleration vector is the rate of change of the velocity vector with time. This includes the direction of the velocity vector. The direction of the radial component of velocity is changing with time, and this results in a component of acceleration in the circumferential direction. This is a term you omitted in your determination of the circumferential acceleration.

 

[Saitama]

Part of the problem is calling it the tangential acceleration. You should be calling it the circumferential acceleration. Here's how the radial component of velocity comes into the picture when calculating the circumferential acceleration. Don't forget that the acceleration vector is the rate of change of the velocity vector with time. This includes the direction of the velocity vector. The direction of the radial component of velocity is changing with time, and this results in a component of acceleration in the circumferential direction. This is a term you omitted in your determination of the circumferential acceleration.

Thanks for the explanation Chestermiller. :)

Using the expression you posted in #5, I get the correct answer.

Since I am not comfortable with polar coordinates, I was finding out an alternative approach to find the torque. I thought of finding the angular momentum of system and find dL/dt to find the torque.

Angular momentum of system at any time t is:
$$L=(I+mr^2)\omega$$
where I is the moment of inertia of rod.
$$\frac{dL}{dt}=2mr\omega \frac{dr}{dt}=2mr_0^2\omega^2e^{2\omega t}$$
Hence power is $(dL/dt)\omega$. Is this a correct approach?

Thank you very much voko and Chestermiller.

 

[Chestermiller]

Yes. This development using the angular momentum works for me. The direction of the angular momentum vector doesn't change with time in this problem.

Chet

 

[Saitama]

Yes. This development using the angular momentum works for me. The direction of the angular momentum vector doesn't change with time in this problem.

Chet

Thanks for the check Chestermiller.