Understanding the Point Of Action of a Force

[tomtomtom1]

TL;DR Summary

Understanding Point Of Action Of A Force

y' = 2/3 * Y

Hello all

I was hoping some could help shed light on the idea of a Point Of Action of a force.

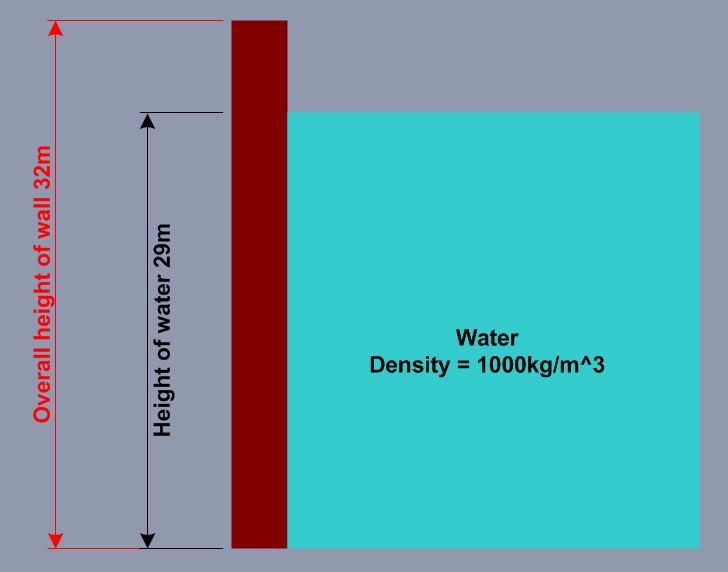
I have a rectangular wall of 32m which is holding back water, the water is at a height of 29m.

Where is the point of action of the force?

The problem is illustrated below:-

I have been told that to find the point of action of the force for a rectangular wall I need to use the following equation:-

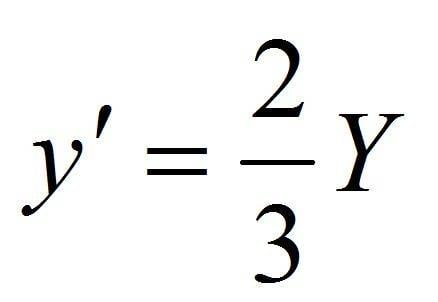I need some help applying this because it does not make a lot a sense to me.

From research and help from the community about other questions, I feel that the point of action should be related to the centroid, but I am struggling to put all the pieces together.

Can anyone help?

Thank you.

 

[jrmichler]

A good way to understand this is to sketch the water pressure vs depth. It helps to put the pressure vs depth sketch on the wall. The centroid of the pressure vs depth sketch is the height of the point of action of the total force.

When working on problems like this, it is a good idea to make a simple sketch of everything you know before looking for an equation. Many times, a good sketch will make the solution obvious, or at least less confusing.

 

[tomtomtom1]

A good way to understand this is to sketch the water pressure vs depth. It helps to put the pressure vs depth sketch on the wall. The centroid of the pressure vs depth sketch is the height of the point of action of the total force.

When working on problems like this, it is a good idea to make a simple sketch of everything you know before looking for an equation. Many times, a good sketch will make the solution obvious, or at least less confusing.

I manage to find the pressure at any point on the wall and was able to find the centroid of the wall itself, this is what I have:-

Still not sure how the equation y' = 2/3 * Y comes from.

I am assuming that y' is the distance from the bottom of the surface of the water to the point of action or y' is from the water surface down to the point of action.

That's all I have.

 

[jrmichler]

There are two centroids, the centroid of the wall itself, and the centroid of the pressure against the wall. Note 2 in the diagram refers to the centroid of the wall itself. It has nothing to do with the centroid of the pressure against the wall.

Imagine that the wall is mounted to a movable hinge. If the hinge is at the top of the wall, the water pressure will swing the bottom of the wall outward. If the hinge is at the bottom of the wall, the water pressure will swing the top of the wall outward. If the hinge is at the centroid of the pressure, the wall will stay in position. Knowing that, and without any math, can you mark the approximate centroid of the pressure? Then, and only then, are you ready to find or derive the equation for the exact location of the centroid of pressure.