monjinho said:
If μ is the ratio of |F| / |R|, how would you get the frictional force in the first place? Wouldn't you need the coefficient of friction? Supposing that there wasn't the coefficient of friction, is it possible that the frictional force could just equal the normal force??
Monjinho,
Physics is based on experience. You have experience of force when you push a crate on the floor, don't you? You need to exert force to move it even with constant speed, so
i. there should be a resistive force between the crate and floor that opposes motion.
Pushing the crate on a smooth surface requires less force than pushing it along a rough one, like concrete.
ii. This resistive force depends on the quality of the surfaces.
You need greater force to push the same crate when it is full of heavy objects than the empty one.
iii. The resistive force depends on the weight of the object.
One can conclude that there is a resistive force that opposes the applied force when an object is moved along a horizontal surface. You call the phenomenon "friction" and the resistive force "force of friction".
You can even measure this force, in an experiment. Connect a spring to a box and pull the spring. The length of the spring increases and the force applied to the box is proportional to the increase of length.
From your experiment, you find an approximate linear relation between the weight of the object and the resistive force, the force of friction. It is interesting, as the weight is a vertical force and the resistance is horizontal, but you experience that their magnitudes are related and proportional to each other.
You ask a friend to push the box downward, and you find that higher force is needed to pull the box now. So you conclude that it is not the weight, but the force that presses the ground, (the normal force between the box and ground) that counts. The magnitude of the resistive force against sliding , the force of friction, is proportional to the magnitude of the normal force. You call this factor of proportionality the "coefficient of friction"
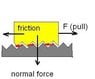
You can think about the cause of this resistive force. What happens if an object slides on a surface? What causes a horizontal force from the vertical one?
The surfaces are not perfectly smooth. See attached picture. If the object moves, the spikes of its surface press against those of the ground, and the spikes of the ground exert force against the object, see the red arrows. In order to slide, the unevenness has to be smoothed out somehow - by tearing the peaks off or press them away. You can see a mark when you push something along a sandy surface, as the grains of sand were moved away or pressed together. A breaking car leaves a skid mark. So there is some interaction between the sliding surfaces that can even permanently change them.
monjinho said:
I guess the main thing i don't understand is how we can get a horizontal force value when we multiply two things that are not related at all by magnitude(direction). If it is simply a scalar force, we still need the direction and need to know where the force is pointing toward for later problems.
Those two things -the normal force and force of friction-
are related , you experience it. There is no such thing as "scalar force". Force is a vector quantity, has both magnitude and direction. The force of friction is caused by the interaction between the sliding surfaces, and points along the surfaces touching each other, and it is opposite to the velocity of the moving object with respect to the surface it moves on.
ehild