Eran
- 5
- 0
Hi,
I thought it would be an easy one but it isn't...
I am trying to solve the problem of a beam supported by three different springs with a uniform distributed load:
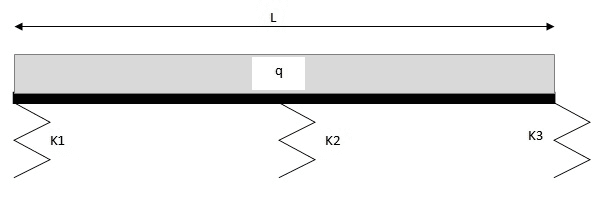
I thought it would be an easy one but it isn't...
I am trying to solve the problem of a beam supported by three different springs with a uniform distributed load: