Unraveling Diffraction: Understanding Variable Relationships

[Hereformore]

I'm having trouble understanding the relationships between various variables at play in diffraction.

Say you have diffraction with one slit, two slits, and a grating as shown below.

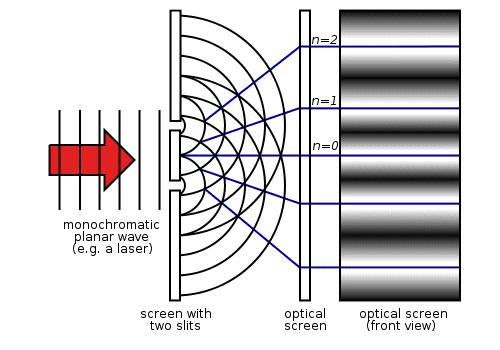
So
1) The Amplitude of each peak is directly proportional to the intensity of the incoming waves. This makes sense.

2) The wavelength is directly proportional to the spacing between peaks.
Is this because as the wavelength gets larger, less interference can occur so the spacing is greater? Versus if the wavelength is smaller, more interference can occur per area so the peak frequency is higher.

3) If you increase the distance between each slit, the spacing between each peak gets shorter.
This I do not understand. I would think that if you increased the spacing in between each slit, that the spacing between peaks would be greater since there is more space in between the starting wavelets.

4) If you increase the distance between the starting screen and optical screen, then the spacing decreases.
Is this because as you increase the distance you give the waves more time to interact and interfere. My text says it is because you are giving the interference pattern more distance over which to spread if you increase the distance L. But that would suggest to me that then the spacing would be greater if the waves are spreading out further

5) If you increase the number of slits, given the same "entering" intensity, then the amplitude of the each peak is greater and sharper. And the spacing in between each peak is greater with a greater number of slits.
The relationship between # of slits and distance between each peak makes sense to me. If you have more slits, then for constructive interference to occur, more waves must interfere the right way to create that peak so there's a lower chance of it happening. Hence there are fewer peaks per area/amount of screen.Regarding peak intensity however, my text says, "Since a fixed amount of light should reach the screen, if the number of spots decreases, the intensity of each remaining spot should increase.". Conversely, if the number of slits increases, you should see lower intensity.

But what we see actually happening is very different:

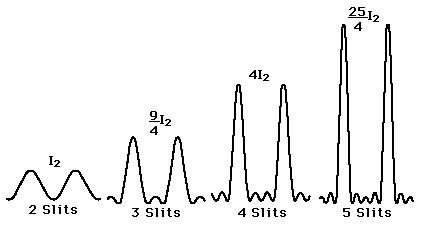
More slits causes greater intensity here. Is it because the effect of having fewer fewer peaks (caused by having more slits) overpowers the effect of having more slits on the intensity of each spot? Also is "sharpness" a factor of brightness here?

Thanks a lot guys. Spent all day trying to understand diffraction here. If there's any relationship I'm missing please tell me!

 

[sophiecentaur]

The basic relationships are far better described using the Maths, which gives you exactly the right answer. Have you looked into the Maths yet? The 'reason' it works the way it does is down the the Path Difference between the route through the two slits to any point on the screen because it is the difference in path length that determines the relative phases of the waves arriving, which determines how the two vectors add (constructive, destructive or somewhere in between). It is not possible to predict the precise shape of the diffraction curve without some Trig involvement but it is possible to show the positions of the maxes and mins fairly easily.
http://schools.matter.org.uk/content/interference/formula.html . and this link are examples of the way the basic two slit diffraction pattern is formed.

 

[Hereformore]

I see. Okay no wonder i was having so much trouble. Thank you. I see the two pages are for double slits. Do the same principles apply to increasing # ofs slits?

Additionally: Regarding maxima intensities i see that the pages say,"
How bright are the maxima you may ask? -- Equal contributions from each of two slits makes the E and B fields twice as large as they would have been with only one slit open. The light intensity (measured in W/m^2) is proportional to E2 and B2, so the maxima have an intensity that is 4 times greater than would be present if only 1 slit were open.

So I think my error in understanding was that all of the incoming light would be "squeezed into" however many number of slits there are. But in reality, it's more like you have ten jellybeans, and X number of slots, each of which take the same amount of time to pass a jelly bean through. So having fewer slots would not allow more jelly beans through per unit time/Area, but rather fewer because the rate limit is constant. But with greater slots open for business, you would get more.

Is is the same case for the # of slits?

 

[olivermsun]

Yeah, it's the same. As you say, the incident intensity is "per area," and what is received at the screen is just the contribution from all the slits.

Also, the sharpness does matter because there's still a conservation of energy at play here.

 

[Hereformore]

Yeah, it's the same. As you say, the incident intensity is "per area," and what is received at the screen is just the contribution from all the slits.

Also, the sharpness does matter because there's still a conservation of energy at play here.

By conservation of energy is between the energy do you mean conservation of energy that goes through the slits and the amount of light that hits the screen? So if you change something OTHER than the number of slits, like wavelength (say increase wavelength), then the distance between the peaks is greater so there should be fewer # of peaks per area. Since energy must be conserved, with fewer peaks (or is it the same number of peaks but thinner peaks?), each peak should be brighter/sharper? (assuming sharper = brighter).

Thanks man this is helping a lot.

 

[olivermsun]

Yeah, that's what I'm thinking of in terms of conservation of energy. All the light in the pattern on the screen has to be equal to the light that goes through the slits.
If you change the wavelength, then hmm… there can be fewer peaks per length, but they can can also be wider, right? I.e., the pattern stretches and shrinks depending on the wavelength, but the total energy received at the screen has to be the same. I'll think about it some more...