MexChemE
- 237
- 54
Homework Statement
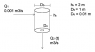
A cylindrical tank, with a diameter Db, open to the atmosphere, is drained through an orifice in the bottom of the tank with a diameter Do. The speed of the fluid flowing through the orifice is given by v = \sqrt{2gh}, where h is the height of the liquid measured from the bottom of the tank.
Calculate the amount of liquid spilled in 10 minutes (600 seconds), when h0 = 2 m, Db = 1 m, and Do = 0.01 m. The tank is also fed with a constant flow of 0.001 m3 s-1.
Homework Equations
\frac{dm}{dt} = \dot{m}_{in} - \dot{m}_{out}
The Attempt at a Solution
I sketched an schematic diagram of the problem, which I attached below. First, since I'm dealing with a pure substance I went ahead and skipped the mass balance and instead started from the dummy volume "balance."
\frac{dV}{dt} = Q_1 - Q_2
But V = Abh and Q2 = Aov. Also, v = \sqrt{2gh}, so:
A_b \frac{dh}{dt} = Q_1 - A_o \sqrt{2gh}
Separating variables and integrating:
\int_{h_0}^h \frac{dh}{\sqrt{h}} = \left( \frac{Q_1}{A_b} - \frac{A_o}{A_b} \sqrt{2g} \right) \int_0^t dt
Yields:
h = \left( \sqrt{h_0} + 0.5 \left( \frac{Q_1}{A_b} - \frac{A_o}{A_b} \sqrt{2g} \right) t \right)^2
Now, calculating both areas yields Ab = 0.785 m2 and Ao = 7.854x10-5 m2. This is where trouble begins. Plugging all given values into h(t) yields h = 2.767 m. I would normally calculate the volume of spilled liquid with:
V_{\textrm{spilled}} = A_b (h_0 - h)
But plugging in these values yields a negative result. Obviously the amount of liquid entering the tank is greater than the amount flowing out, but then, how does one measure the amount of the spilled liquid only? Also, I'm assuming unlimited tank capacity. I tried integrating the exiting flow:
V_{\textrm{spilled}} = \int_0^{600} Q(t) dt = A_o \sqrt{2g} \int_0^{600} \sqrt{h}(t) \ dt
But it yielded the same negative result. Any ideas?
Thanks in advance for any input!
Attachments
Last edited: