karush
Gold Member
MHB
- 3,240
- 5
$\tiny{up 244.14.4.26}$
$\textit{a. Sketch the region of Intregration}$
$\textit{b. convert the sum of integrals to a Cartesian sum of Integrals:}$
\begin{align*}\displaystyle
I_{26}&=\int_{0}^{\tan^{-1}(4/3)}
\int_{0}^{3\sec{\theta}}
r^7 \, dr \, d\theta
+\int_{\tan^{-1}(4/3)}^{\pi/2}
\int_{0}^{4\csc\theta}
r^7 \, dr \, d\theta\\
&=\int_{0}^{\tan^{-1}(4/3)}\Biggr|\frac{r^8}{8}\Biggr|_0^{3\sec{\theta}} \, d\theta
+\int_{\tan^{-1}(4/3)}^{\pi/2}\Biggr|\frac{r^8}{8}\Biggr|_{0}^{4\csc\theta} \, d\theta
\end{align*}
next ?
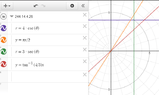
OK first I don't how you plot $r^7$ on Desmos
$\textit{a. Sketch the region of Intregration}$
$\textit{b. convert the sum of integrals to a Cartesian sum of Integrals:}$
\begin{align*}\displaystyle
I_{26}&=\int_{0}^{\tan^{-1}(4/3)}
\int_{0}^{3\sec{\theta}}
r^7 \, dr \, d\theta
+\int_{\tan^{-1}(4/3)}^{\pi/2}
\int_{0}^{4\csc\theta}
r^7 \, dr \, d\theta\\
&=\int_{0}^{\tan^{-1}(4/3)}\Biggr|\frac{r^8}{8}\Biggr|_0^{3\sec{\theta}} \, d\theta
+\int_{\tan^{-1}(4/3)}^{\pi/2}\Biggr|\frac{r^8}{8}\Biggr|_{0}^{4\csc\theta} \, d\theta
\end{align*}
next ?
OK first I don't how you plot $r^7$ on Desmos
Last edited: