Upper Bound Theorem: Verifying Inequality & Non-Planarity

[Natasha1]

The converse of the Upper Bound Theorem would state that a graph which satisfies the inequality

$$e \leq { \frac{n (v-2)}{n-2}$$ is planar.

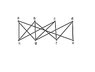
This converse is not true as seen in picture.

Verify that the inequality $$e \leq { \frac{n (v-2)}{n-2}$$ is true for this graph.

Using the inside-outside algorithm to show that the graph is actually non-planar.

 

[Natasha1]

Does anyone know what the n stands for?

 

[Natasha1]

e = edges
v = vertices

but what is n?

 

[0rthodontist]

There is more than one "upper bound theorem" and more than one "inside-out algorithm." Why don't you start by stating them here? This will help you as well as me. Your book should tell you what n is in the theorem statement.

 

[Natasha1]

Even using google doesn't help me to understand what n is?

 

[0rthodontist]

Yes, so look in your book.

 

[Natasha1]

Not in my book

 

[matt grime]

It will be explained wherever you got the question from.

 

[shmoe]

I'll take a guess- perhaps n is the smallest cycle. This would correspond to the face with the smallest number of edges in a planar graph*, so you would have n<=2e/f. Apply Euler's to get rid of f (this is assuming planar) and fiddle around and you can get the inequality you've posted.

But yea, this should be in your book, notes, or wherever this problem is from, so find it in your materials as my guess may not be what they are after (though it does look like it).*edit- this isn't quite right, but the minimal cycle length is <= the smallest number of edges on a face and the rest is the same.