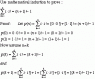You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Use mathematical induction to prove:
- Thread starter nddewaters
- Start date
Physics news on Phys.org
Mark44
Mentor
- 38,043
- 10,530
What have you tried?
Mark44
Mentor
- 38,043
- 10,530
You are using induction correctly, but you have a mistake.
Your induction hypothesis for n = k is
\sum_{i = 1}^k \frac{1}{i(i + 1)} = \frac{k}{k + 1}
For n = k + 1 we have
\sum_{i = 1}^{k + 1} \frac{1}{i(i + 1)} = \sum_{i = 1}^k \frac{1}{i(i + 1)} + \frac{1}{(k + 1)(k + 2)}
The last expression on the right is where you made your mistake. You have k + 1. What you should have is the value of 1/(i(i + 1)) when i = k + 1.
BTW, the font size in your attachment is very small, almost too small for my old eyes to read.
Also, if you click either of my equations above, you can see my LaTeX script.
Your induction hypothesis for n = k is
\sum_{i = 1}^k \frac{1}{i(i + 1)} = \frac{k}{k + 1}
For n = k + 1 we have
\sum_{i = 1}^{k + 1} \frac{1}{i(i + 1)} = \sum_{i = 1}^k \frac{1}{i(i + 1)} + \frac{1}{(k + 1)(k + 2)}
The last expression on the right is where you made your mistake. You have k + 1. What you should have is the value of 1/(i(i + 1)) when i = k + 1.
BTW, the font size in your attachment is very small, almost too small for my old eyes to read.
Also, if you click either of my equations above, you can see my LaTeX script.
nddewaters
- 6
- 0
Mark44
Mentor
- 38,043
- 10,530
For starters, you have a typo in your summation. It should be
\sum_{i = 1}^n i\cdot i!
The index for your summation is i, not o or 0.
Your induction hypothesis is
\sum_{i = 1}^k i\cdot i! = (k + 1)! - 1
This is the statement when n = k
The statement you're trying to prove, when n = k + 1, is
\sum_{i = 1}^{k + 1} i\cdot i! = (k + 2)! - 1
and not what you have.
\sum_{i = 1}^n i\cdot i!
The index for your summation is i, not o or 0.
Your induction hypothesis is
\sum_{i = 1}^k i\cdot i! = (k + 1)! - 1
This is the statement when n = k
The statement you're trying to prove, when n = k + 1, is
\sum_{i = 1}^{k + 1} i\cdot i! = (k + 2)! - 1
and not what you have.
Last edited:
nddewaters
- 6
- 0
Mark44 said:For starters, you have a typo in your summation. It should be
\sum_{o = 1}^n i\cdot i!
The index for your summation is i, not o or 0.
Your induction hypothesis is
\sum_{i = 1}^k i\cdot i! = (k + 1)! - 1
This is the statement when n = k
The statement you're trying to prove, when n = k + 1, is
\sum_{i = 1}^{k + 1} i\cdot i! = (k + 2)! - 1
and not what you have.
Could you now help me in getting the algebra started that is required to finish the proof?
Thank You
Mark44
Mentor
- 38,043
- 10,530
\sum_{i = 1}^{k + 1} i\cdot i! = \sum_{i = 1}^{k} i\cdot i! + (k + 1)(k + 1)!
Similar threads
- Replies
- 6
- Views
- 2K
- Replies
- 4
- Views
- 2K
- Replies
- 2
- Views
- 2K
- Replies
- 7
- Views
- 1K
- Replies
- 7
- Views
- 2K
- Replies
- 7
- Views
- 1K
- Replies
- 4
- Views
- 2K
- Replies
- 5
- Views
- 2K
- Replies
- 5
- Views
- 2K
- Replies
- 3
- Views
- 2K
Hot Threads
-
Prove that the integral is equal to ##\pi^2/8##
- Started by Meden Agan
- Replies: 105
- Calculus and Beyond Homework Help
-
Limit of piecewise function using epsilon delta
- Started by songoku
- Replies: 31
- Calculus and Beyond Homework Help
-
Dot diagrams and Jordan canonical forms
- Started by psie
- Replies: 3
- Calculus and Beyond Homework Help
Recent Insights
-
Insights Thinking Outside The Box Versus Knowing What’s In The Box
- Started by Greg Bernhardt
- Replies: 3
- Other Physics Topics
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 28
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 3
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math