TheRealDoodle
- 3
- 0
Homework Statement
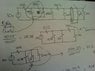
Use resistor simplification to find current across the 10ohm resistor
Homework Equations
V=ir p=vi
The Attempt at a Solution
Any help you can give me is much appreciated. When I did it i got down to a parallel circuit with a 30ohm and a 100ohm but didnt get a round answer and i thought the teacher said theyre all rigged to come out right.



 Missed that, thanks for spotting it.
Missed that, thanks for spotting it.