mm2424
- 43
- 0
Homework Statement
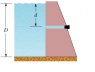
Consider the fresh water damn shown in the picture (attached below). The water behind the dam has depth D = 15 m. A horizontal pipe 4 cm in diameter passes through the dam at depth d = 6 m. A plug secures the opening. The plug is removed. Water water volume exits the pipe in 3 hours?
Homework Equations
p(atmosphere) + ρgh1 + 1/2ρ(v1)^2 = p(atmosphere) + ρgh2 + 1/2ρ(v2)^2
The Attempt at a Solution
I'm treating the left side of the equation as the water in the reservoir and the right hand of the equation as the water flowing through the hole.
I began by simplifying Bernoulli's equation, cancelling out the p(atmosphere) and the density of water. I also remove the 1/2(v1)^2 term, assuming v1 is very small:
gh1 = gh2 + 1/2(v2)^2
I start to get confused in terms of the heights I should be using here.
Is h1 the full height of the water (15 m)? The answer key in my book seems to treat h1 as the full height of the water (15 m), but that confuses me, since it seems like the center of mass of the water would only be 7.5 m up.
I assume h2 is the height of the water in the pipe, which is about 9 m (15 m - 6 m).
I'm confused because if I trust my reasoning and use the center of mass of the water, v2 is negative, which of course makes no sense.
Am I missing something here? Is there some reason why I should consider h1 to be 15 m, despite the fact that most of the water isn't really 15 m up?
Thanks!
(ps, v2 is supposed to be 10.84 m/s^s, making the final answer 147 m^3.
Attachments
Last edited: