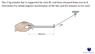
Pipsqueakalchemist said:
In my attempt I assumed the bar was undergoing centripetal motion around the fixed end of the rope
This is hard to believe. I can understand that point B on the bar is constrained to move on a circle around C (*), but point A isn't going to stay on a line that makes an angle of 30 degrees wrt the cord.
(*) provided the cord stays taut, which I think is a reasonable assumption in this case
The word centripetal means 'going towards the center'. It is confusing and ambiguous to use it to describe a movement. When there is a centripetal force acting, a point mass can execute a circular motion.
Let me go back to your first attachment, which I assume is the problem statement:
can you find the force that has to be executed at A to keep the bar in position before it is released ? (**)
And your second attachment (looks as if it is part of the solutions manual ?) seems to be missing something on the righthand side
I assume this is at t=0
after releasing. On the left I see two forces, on the right I see two accelerations. Fine, but I don't see how there can be an equals sign in between.
[edit] my mistake. The 2 means 2 kg and then the purple arrows are forces too.
Still I can't explain the equals sign.
At t=0 the force you calculated at (**), is instantly removed. You have to ask yourself if it is reasonable to expect that T does not change instantly. If it doesn't, you have two forces that will cause the bar to drop and rotate. Choose an axis of rotation (***) and work out ##\alpha##, the angular acceleration.
Re
I can follow the first three lines, but the fourth ?
What is I ? Moment of inertia. Expression ?
##v_{B/A}## is what ? velocity of B wrt A ? Vector ? Scalar ?
##\omega## ?
(***) line three makes me think you picked G ?
##\ ##