Using energy methods in a moment of inertia problem?

[erik-the-red]

Question

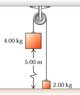
The pulley in the attachment has radius 0.160 m and a moment of inertia 0.480 {\rm kg} \cdot {\rm m}^{2}. The rope does not slip on the pulley rim.

1. Use energy methods to calculate the speed of the 4.00-kg block just before it strikes the floor.

I'm thinking: K_1 + U_1 = K_2 + U_2.

I'm also thinking that K_1=U_2=0, which implies U_1=K_2.

Then, mgh=(1/2)(m)(v^2). Solving for v, I get v=\sqrt(2*9.80*5)=9.90 m/s.

But, this isn't correct.

What did I do wrong?

 

[arildno]

And where have you included the kinetic energy the pulley itself has?
The energy of the block itself is not conserved, but the energy of the system block+pulley is.

 

[erik-the-red]

And where have you included the kinetic energy the pulley itself has?
The energy of the block itself is not conserved, but the energy of the system block+pulley is.

K_p=(1/2)(I)(\omega)^2.
K_p=(1/2)(I)(v/r)^2

Energy system of the block and pulley?

K_1 + U_1 + K_(p_1) = K_2 + U_2 + K_(p_2)

U_1 = K_2 + K_(p_2)

mgh = (1/2)(m)(v_2)^2 + (1/2)(I)(v_2/r)^2
(4.00)(9.80)(5.00) = (1/2)(4.00)(v_2)^2 + (1/2)(.480)((v_2)^2/(.160^2))
v_2 = 4.15 m/s.

Is my reasoning correct?

 

[arildno]

It should be, given the information you've given me.

 

[erik-the-red]

:(

4.15 m/s is not correct.

I didn't think about the rotational kinetic energy, so obviously my initial answer was not correct.

I guess I must have figured it in incorrectly, but I don't know why I am wrong.

 

[arildno]

But state the problem PRECISELY!
For example, is there a lighter block in the picture that travels upwards as the 4.0 kg block travel downwards?
You didn't inform me on this.
In that case, energy is conserved for the ENTIRE system consisting of the two blocks plus the pulley.

 

[lightgrav]

How do you know 4.15 m/s is not correct?
books sometimes have wrong answers in them.
Your procedure is now correct, and if the block falls 5 m, your answer is, too.

On the other hand, if this pulley is "attached" to something that might move, that MUST be taken into account!

 

[erik-the-red]

Thanks to everyone who replied. You made me realize that I forgot to attach a picture, but more importantly, that I forgot to take into account an object that indeed might move!

I will reconsider this problem now.

 

[arildno]

I think the possibility that the other block might move can be made into a certainty..
Good luck!
Hint:
Be careful about the gravitational potential energy terms, get them right!

 

[erik-the-red]

Thanks, I got this question right.

The general form was K_1 + U_1 + K_1 + U_1 + K_R = K_2+ U_2 + K_2 + U_2 + K_R.

Note that the equation I listed isn't the one I used, it's because I'm still a newb to LaTeX that I couldn't differentiate between object A of mass 4.00kg and object B of mass 2.00kg.

A bunch of terms canceled out and I got the answer.