I Getting the sign right with the work-energy theorem

[Rick16]

TL;DR Summary

getting the sign right with the work-energy theorem

This is problem 3 in section 2.3.4 from Conquering the Physics GRE by Kahn and Anderson:

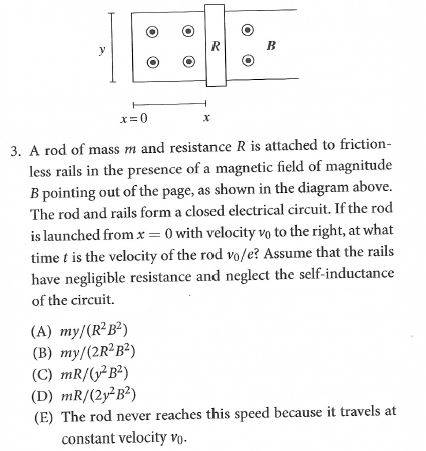
And here is the solution from the book:

The point of confusion for me is that they use the work-energy theorem in the form W = T_initial - T_final, instead of the other way around. If I were to do this problem, I would write W = T_final - T_initial, but then I end up with a negative time, which does not make sense. What am I missing?

 

[TSny]

You are right that the work performed on the rod should be $W = \dfrac 1 2 m \dot x^2 - \dfrac 1 2 m \dot x_0^2$. So, the text has a sign error here.

But $P = \mathcal{E}^2/R$ gives the rate at which KE of the rod is transformed into Joule heat in $R$. So, $P$ equals the rate of loss of KE of the rod. Thus, $P = -\dfrac {d}{dt} (KE)_{\rm rod}= - \dfrac {dW} {dt}$. So, the text has an additional sign error here that compensates for the first error.

The print in the margin of the image is blurred, so I'm assuming $W$ is the work done on the rod.

 

[Rick16]

Thanks a lot! I constantly run into problems with minus signs. I think they make up 98% of all the mistakes that I make. It's very frustrating. And yes, the text says "the work performed on the rod". Sorry about the bad quality of the scan. I scanned the page several times and this is the best that I could do.