- #1
ektov_konstantin
- 5
- 0
- TL;DR Summary
- I have a physically correct approach but I get incorrect result and need some help!
Hello, everyone!
I am calculating the time of substrates' heating in the vacuum chamber.
It is a simple mathematical model to calculate roughly how much time does it take to heat polycor substrates in the vacuum chamber.
At least all the tube heater`s power heats the substrates (this is because the geometry of the vacuum chamber and beacuse all inner surface is polished).
So our goal is to get the time when conductive heating will be equal to the radiative heat losses.
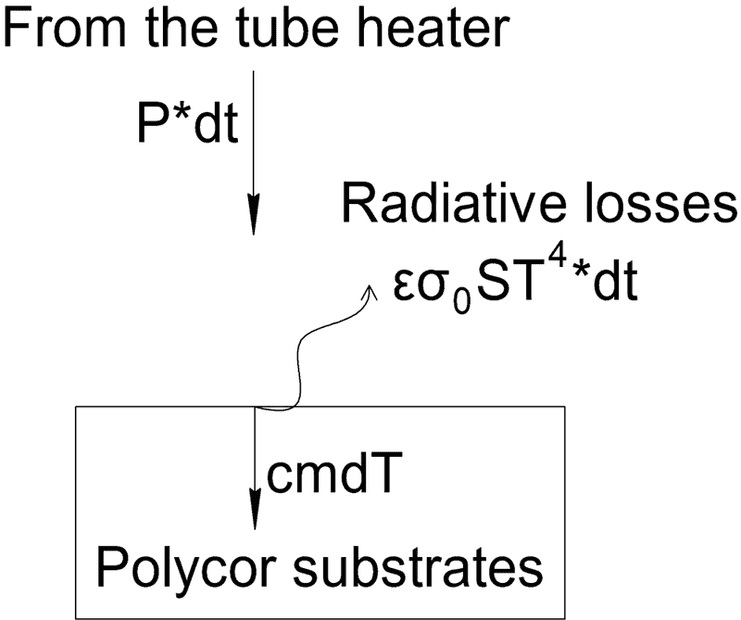
Look at the scheme.
So the differential equation is .
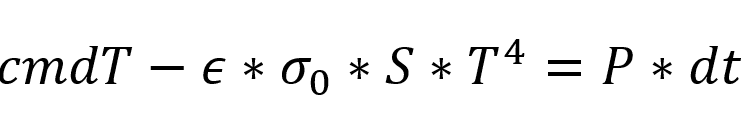
And dividing the variables we get
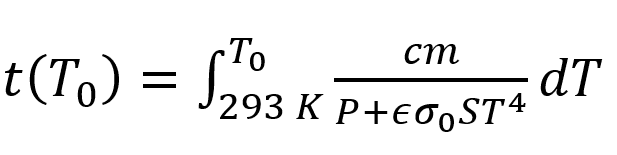 , where T_0 is the Temperature when conductive heating equals radiative losses.
, where T_0 is the Temperature when conductive heating equals radiative losses.
If P=800 W, I have this dependence...
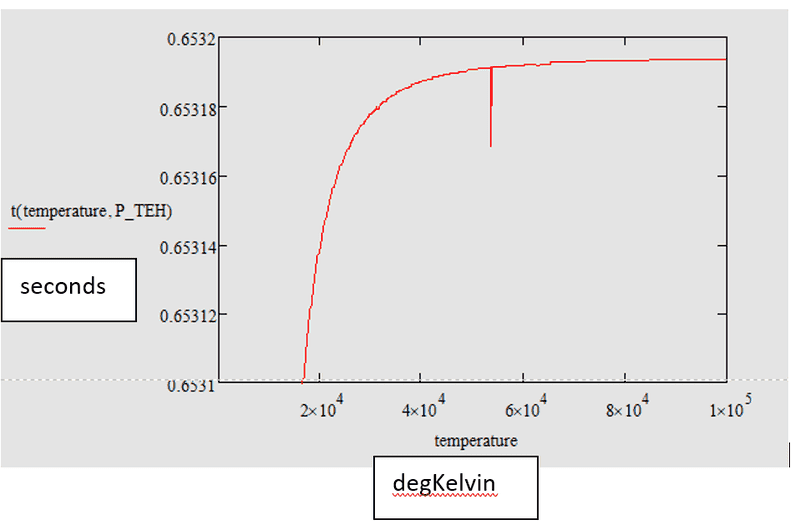
and as you can see, it is not physically right beacuse of two reasons. First - why there is a horisontal asymptote (it must be vertical!) ? Second - the heating is very-very fast...
For instance, I have calculated the heating time if there are no radiative losses.
t = c*m*(T_0-293)/W
and for W=800 W, T_0=623 K (technological process` temperature) we get t=0,205 seconds - and it is rubbish too I think...
Additionaly I add the constants and variables that I have used in my MathCAD app.

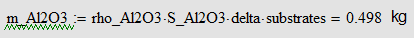
I am calculating the time of substrates' heating in the vacuum chamber.
It is a simple mathematical model to calculate roughly how much time does it take to heat polycor substrates in the vacuum chamber.
At least all the tube heater`s power heats the substrates (this is because the geometry of the vacuum chamber and beacuse all inner surface is polished).
So our goal is to get the time when conductive heating will be equal to the radiative heat losses.
Look at the scheme.
So the differential equation is .
And dividing the variables we get
If P=800 W, I have this dependence...
and as you can see, it is not physically right beacuse of two reasons. First - why there is a horisontal asymptote (it must be vertical!) ? Second - the heating is very-very fast...
For instance, I have calculated the heating time if there are no radiative losses.
t = c*m*(T_0-293)/W
and for W=800 W, T_0=623 K (technological process` temperature) we get t=0,205 seconds - and it is rubbish too I think...
Additionaly I add the constants and variables that I have used in my MathCAD app.