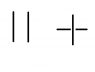Van der waals attraction between 1-D wires

[CAF123]

Homework Statement

Consider two infinitesimally thin (i.e 1-D) wires of equal length $L$, and at
mutual distance $d$.
Consider the two configurations shown in attachment
Estimate the van der Waals interaction between the wires, for $d \gg L$, in the two situations

where: (i) the wires are parallel and in register, as on left and (ii) the wires lie on parallel
planes and are in the ''cross'' configuration as on the right.

Homework Equations

VDW attraction between atoms modeled by $u(r) = - C/r^6, C$ a constant.

The Attempt at a Solution

Set up a coordinate system with $z$ axis coinciding with the wire with origin midway. The attraction between the atom at $z=0$ on one wire and an arbritary atom at some distance $\sqrt{d^2 + z^2}$ is therefore $u(z) = -C/(z^2 + d^2)^3$. This atom at $z=0$ therefore contributes $U(r) = \int_{-L/2}^{L/2} u(z) dz$, i.e the interaction energy contributed from this atom on one wire and all others on the other. Now how should I proceed to get the total interaction energy due to all atoms? I wasn't specified the atom density along the wires.

I can't make sense of the mutual distance of the wires being a distance $d$ apart in the second configuration.

Thanks.

 

[CAF123]

The question was updated with the atomic density being $\sigma$, so my answer for the total interaction energy between the wires is $\sigma L U(r)$ Is it correct?

 

[CAF123]

Can anyone help?