clickcaptain
- 31
- 0
Given F = (-20i + 50j = 10k)
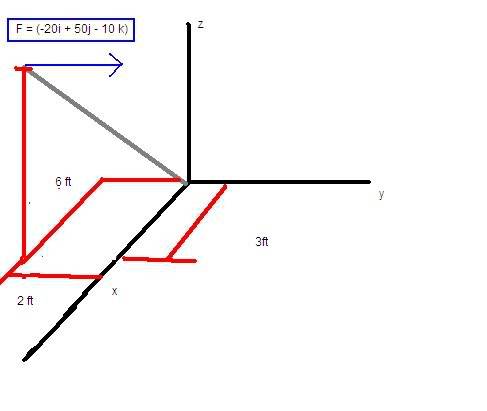
1. The component of the foce projected along the pole AO.
2. The magnitude of the projected component of the F along the pole AO.
I have no idea where to begin, I think I need to find the angles but I'm not sure how in three dimensions.
(please excuse the picture...i know its not the greatest)
1. The component of the foce projected along the pole AO.
2. The magnitude of the projected component of the F along the pole AO.
I have no idea where to begin, I think I need to find the angles but I'm not sure how in three dimensions.
(please excuse the picture...i know its not the greatest)