jrcdude
- 16
- 0
Homework Statement
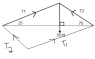
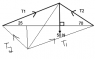
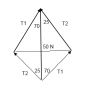
A 50 N sign is suspended by two cables that make angles of 25 degrees and 70 degrees with the horizontal. Determine the tension in each cable.
Homework Equations
Cosine law, sine law, or trig
The Attempt at a Solution
I believe that the teacher's answer is wrong. She did it the same way as the following person:
I did it with the exact same diagram, same angles, but instead of using sine and cosine law, I just used normal trig and divided the tension in half for the triangle's vertical component, resulting in a different answer for the tensions.
This leads me to the conclusion that both answers are wrong, because you cannot just assume there is a 90 degree angle for where the tension hits the horizontal.
Is this assumption correct, and can I have a proper way to do this, with a proper answer?