Taylor_1989
- 400
- 14
- TL;DR
- Trying to understand the origin of a velocity equation by deriving it.
I was not really sure as to whether to ask this question here or the h/w forum as its something I am personally trying to understand. However, I shall let the admin decided.
The question comes from a book called :
Here is the actual question along with the given diagram:
As depicted in Fig. P5.15, the velocity of water, v(m/s)v(m/s), discharged from a cylindrical tank through a long pipe can be computed as:
##v=\sqrt{\left(2gH\right)}\cdot tanh\left(\frac{\sqrt{\left(2gH\right)}}{2L}t\right)##Diagram
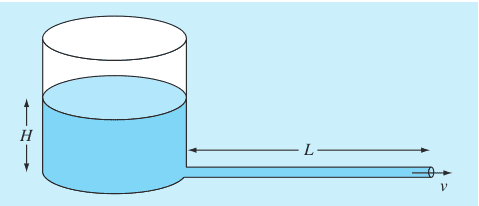
What I have been trying to figure is where this equation comes from. Now granted my fluids knowledge is not fantastic, which is why I am trying to figure out how to derive this equation as a learning opportunity.
So in my effort to try and derive the equation I have been using an old text I used in the past along with a lab report I found online, but I am still drawing blanks in how this equation been derived.
The lab report I found online is given by the following link: https://www.ias.ac.in/article/fulltext/reso/023/01/0069-0081
Now reading through this report section 3.
seems to have some relevance maybe on what I should be looking into but I can't seem to take the next steps and form the hyperbolic part of the equation.
I do have a working knowledge of fluids of Bernoulli’s Equation etc and the book I normally use a resource to anything fluids is
Which actually have and exercise where you have to calculate the exit velocity but only uses Bernoulli’s Equation to do so.
If anyone could give me some idea on an approach to deriving this equation or where I should be looking to learn how to derive it, I would be much grateful.
The question comes from a book called :
. The specific question I have an issue with is not the question itself but the equation given within the actual question. For those of have access to the book, it is on page 142, prob 5.15.Numerical Methods for Engineers by Steven C.Chapra and Raymond P.Canale
Here is the actual question along with the given diagram:
As depicted in Fig. P5.15, the velocity of water, v(m/s)v(m/s), discharged from a cylindrical tank through a long pipe can be computed as:
##v=\sqrt{\left(2gH\right)}\cdot tanh\left(\frac{\sqrt{\left(2gH\right)}}{2L}t\right)##
What I have been trying to figure is where this equation comes from. Now granted my fluids knowledge is not fantastic, which is why I am trying to figure out how to derive this equation as a learning opportunity.
So in my effort to try and derive the equation I have been using an old text I used in the past along with a lab report I found online, but I am still drawing blanks in how this equation been derived.
The lab report I found online is given by the following link: https://www.ias.ac.in/article/fulltext/reso/023/01/0069-0081
Now reading through this report section 3.
Modification of (9) Using the Hagen–Poiseuille Equation
seems to have some relevance maybe on what I should be looking into but I can't seem to take the next steps and form the hyperbolic part of the equation.
I do have a working knowledge of fluids of Bernoulli’s Equation etc and the book I normally use a resource to anything fluids is
Fluid Mechanics: Fundamentals and Applications by Yunus A.Cegal and John M.Cimbla
Which actually have and exercise where you have to calculate the exit velocity but only uses Bernoulli’s Equation to do so.
If anyone could give me some idea on an approach to deriving this equation or where I should be looking to learn how to derive it, I would be much grateful.
Last edited: