Velocity of uniform circular motion

[Govind_Balaji]

Homework Statement

The minute hand of a clock is 4cm long. Find the average velocity of the tip of the minute hand between 11.00 am to 11.30 am. (in m/s)

Homework Equations

The Attempt at a Solution

1.In the motion between 11 am to 11.30 am,
<br /> \theta=180^o=\pi \text{radiaans}\\<br /> radius=4cm\\<br /> time=30 min\\<br />

Am I right till now?

<br /> \begin{align*}<br /> v&amp;=\frac{R\theta}{t}\\<br /> &amp;=\frac{4\pi}{30}cm/min\\<br /> &amp;=\frac{4\pi}{30*60*100}m/s\\<br /> &amp;=\frac{3.14}{45000}m/s\\<br /> &amp;=\frac{3.14}{4.5}10^{-5}m/s\\<br /> &amp;=0.69*10^{-5}m/s\\<br /> \end{align*}<br />

But in the book it was given $4.4*10^{-5}m/s$

 

[Nathanael]

I made the same mistake as you, but the problem is more simple than it seems:

Average velocity = Total displacement / total time

The total displacement is not 0.04pi meters, (even though that is the length of the path,) the total displacement is simply the diameter.
P.S.

<br /> \begin{align*}<br /> &amp;=\frac{3.14}{45000}m/s\\<br /> &amp;=\frac{3.14}{4.5}10^{-5}m/s\\<br /> \end{align*}<br />

It would actually be:
\begin{align*}
&=\frac{3.14}{4.5}10^{-4}m/s\\
\end{align*}
Your final answer was small by a factor of 10

 

[Govind_Balaji]

I made the same mistake as you, but the problem is more simple than it seems:

Average velocity = Total displacement / total time

The total displacement is not 0.04pi meters, (even though that is the length of the path,) the total displacement is simply the diameter.



P.S.

It would actually be:
\begin{align*}
&=\frac{3.14}{4.5}10^{-4}m/s\\
\end{align*}
Your final answer was small by a factor of 10

Thanks I got it. $v=\frac{8}{30}\text{cm/min}$. Converting to m/s, I got the same answer.

P.S
I saw that the formula I first used, can only be used for finding speed as it takes distance into account. Is there any other formula which calculates displacement between two points of an arc?

 

[BvU]

Yes. As you knew, arc AB is $R\theta$. Now for line segment AB, you notice A0B is an isoceles triangle. Think half-angle and presto! An expression that is easily checked for your $\theta = \pi$.

 

[Govind_Balaji]

Yes. As you knew, arc AB is $R\theta$. Now for line segment AB, you notice A0B is an isoceles triangle. Think half-angle and presto! An expression that is easily checked for your $\theta = \pi$.

Uh. I am unable to find it. I am just 9th grade.

 

[Nathanael]

Uh. I am unable to find it. I am just 9th grade.

Do you know any triginometry? If you know a bit (which I think you do) then you might be able to use the picture that BvU attatched and do a little trig/geometry to find out that length.

 

[Govind_Balaji]

Do you know any triginometry? If you know a bit (which I think you do) then you might be able to use the picture that BvU attatched and do a little trig/geometry to find out that length.

No I am not taught any trignometry till now in schools. But I have heard about it through some videos and articles in internet. I just know about **SOHCAHTOA**. I don't even know why they are used for.

P.S.:Knowing about the length AB is not about my homework. I just wanted to know about it out of curiosity. I don't think any of rules will be violated if you say me the formula. I just ask only one formula. I googled and yahood it. I can't find anything.

 

[dauto]

No I am not taught any trignometry till now in schools. But I have heard about it through some videos and articles in internet. I just know about **SOHCAHTOA**. I don't even know why they are used for.

P.S.:Knowing about the length AB is not about my homework. I just wanted to know about it out of curiosity. I don't think any of rules will be violated if you say me the formula. I just ask only one formula. I googled and yahood it. I can't find anything.

I find Mnemonics more trouble than they are worth. Try cutting the triangle in half and using your SOHCAHTOA to find the relationship between half the arc to half the angle. If you can't do that then your SOHCAHTOA is as good as nothing. Memorizing a relationship without understanding it won't help you.

 

[Govind_Balaji]

I know sin is Opp./Hyp., cos is Adj./Hyp. and tan is Opp./Adj. I learned them just today through Educator.com 's free 1 year membership, which I got today through PF.

Tell me what should I find sin, cos or tan?

 

[phyzguy]

I made the same mistake as you, but the problem is more simple than it seems:

Average velocity = Total displacement / total time

By this argument the average velocity of the Earth over the course of one year is zero. If you drive from New York to San Francisco and back would you agree that your average velocity during the trip was zero? I would argue that the way the OP did it at first makes more sense.

 

[Nathanael]

By this argument the average velocity of the Earth over the course of one year is zero. If you drive from New York to San Francisco and back would you agree that your average velocity during the trip was zero? I would argue that the way the OP did it at first makes more sense.

I agree, and that's why I did it the same way the OP did too, but that's not what the answer was. I agree (Dislplacement)/(total time) is oversimplified, but nevertheless, it is the most basic meaning of "Average velocity"

The average velocity in both the cases you said would technically be zero (the directions of the vectors all cancel). The average speed, however would not be zero. The average speed would be more interesting/useful.

He is in 9th grade though, so you can expect the most simplified meanings, and velocity deals with displacement, and the average deals with the total.

No I am not taught any trignometry till now in schools. But I have heard about it through some videos and articles in internet. I just know about **SOHCAHTOA**. I don't even know why they are used for.

I agree with the other guy, memorizations are only trouble. If you use it often enough you'll naturally remember it, and if you don't use it often enough, then you don't need to remember it. (Trust me, you WILL use trig enough to naturally remember it. It's a very useful subject.)
I do understand though, that you're just first being exposed to it, so don't worry too much about it, just try to understand as much as possible.

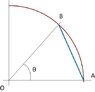
P.S.:Knowing about the length AB is not about my homework. I just wanted to know about it out of curiosity. I don't think any of rules will be violated if you say me the formula. I just ask only one formula. I googled and yahood it. I can't find anything.

I could give you the formula but there's no use in knowing it if you didn't find it yourself. I can tell you, you can find it with the pythagorean theorem and an understanding of what cos(θ) and sin(θ) mean
(radius*cos(θ) is the x-coordinate and radius*sin(θ) is the y-coordinate of the point on the circle at angle θ)
(If that wasn't clear, don't worry, because it's a bit difficult to say with words since you don't know much trig yet, but you'll find it's a very simple idea.)

I don't want to go into a full blown trigonometry lesson, but just try to identify as many lengths as you can in the picture and see if you can find a way to use pythagorean's theorem.


Edit:
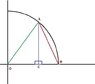
I should have mentioned, in BvU's attatched thumbnail, it will be useful to draw a line straight down from "B" to make two right triangles.

Also what I was trying to say is that point "B" will have (x,y) coordinates ( r*cos(θ), r*sin(θ) )
That is essentially the definition of sin and cos (or it's at least ONE definition, there are many ways to describe the same thing)

 

[dauto]

By this argument the average velocity of the Earth over the course of one year is zero. If you drive from New York to San Francisco and back would you agree that your average velocity during the trip was zero? I would argue that the way the OP did it at first makes more sense.

Well, that's the difference between velocity and speed. The average velocity in the examples you provide is indeed zero. What the OP calculated at first is called average speed.

 

[dauto]

I know sin is Opp./Hyp., cos is Adj./Hyp. and tan is Opp./Adj. I learned them just today through Educator.com 's free 1 year membership, which I got today through PF.

Tell me what should I find sin, cos or tan?

Look at the picture in post # 4. cut the triangle in half so that the angle at the center of the circle is split in half. That produces two identical smaller triangles. Those triangles are square triangles. and the angle at the center is now θ/2, assuming it was θ before being split in two. what's the sine of θ/2 ?

 

[Govind_Balaji]

I should have mentioned, in BvU's attatched thumbnail, it will be useful to draw a line straight down from "B" to make two right triangles.

Also what I was trying to say is that point "B" will have (x,y) coordinates ( r*cos(θ), r*sin(θ) )
That is essentially the definition of sin and cos (or it's at least ONE definition, there are many ways to describe the same thing)

Thank you. I uploaded an attachment. I simplified to

<br /> \\AC=r\sin \theta\\<br /> BC=OB-OC\\<br /> BC=(r)-(r\cos \theta)\\<br />

<br /> AB=\sqrt{(r \sin \theta)^2+(r-r\cos\theta)^2}\\\\<br /> <br /> =\sqrt{r^2 (\sin \theta)^2+r^2+r^2(\cos\theta)^2-2r^2\cos\theta}\\\\<br /> <br /> =\sqrt{r^2 (\sin \theta)^2+r^2+r^2(\cos\theta)^2-2r^2\cos\theta}\\\\<br /> <br /> =\sqrt{r^2\left((\sin\theta)^2+1+(\cos\theta)^2-2\cos\theta\right)}\\\\<br /> <br /> =r\sqrt{(\sin\theta)^2+1+(\cos\theta)^2-2\cos\theta}\\<br />Is there any way to simplify further?

 

[Nathanael]

Thank you. I uploaded an attachment. I simplified to

<br /> \\AC=r\sin \theta\\<br /> BC=OB-OC\\<br /> BC=(r)-(r\cos \theta)\\<br />

<br /> AB=\sqrt{(r \sin \theta)^2+(r-r\cos\theta)^2}\\\\<br /> <br /> =\sqrt{r^2 (\sin \theta)^2+r^2+r^2(\cos\theta)^2-2r^2\cos\theta}\\\\<br /> <br /> =\sqrt{r^2 (\sin \theta)^2+r^2+r^2(\cos\theta)^2-2r^2\cos\theta}\\\\<br /> <br /> =\sqrt{r^2\left((\sin\theta)^2+1+(\cos\theta)^2-2\cos\theta\right)}\\\\<br /> <br /> =r\sqrt{(\sin\theta)^2+1+(\cos\theta)^2-2\cos\theta}\\<br />


Is there any way to simplify further?

Imagine a circle of radius 1 (which they call the "unit circle," you'll learn all about it in trig.)
Sin(θ) is the y coordinate (a.k.a. the height of the leg) and cos(θ) is the x coordinate (a.k.a. the length of the other leg).
From the pythagorean theorem (since it's clearly a right triangle, and as I said, the radius (a.k.a. hypotenuse) is 1) you can derive the formula:
sin^{2}(θ)+cos^{2}(θ)=1 (you'll learn much about this as well)

Therefore you can simplify:
<br /> =r\sqrt{(\sin\theta)^2+1+(\cos\theta)^2-2\cos\theta}\\<br />
into:
<br /> =r\sqrt{2-2\cos\theta} = r\sqrt{2(1-\cos\theta)}\\<br />

There are various ways to rewrite cos(θ) (as you'll learn in trig.) but I can't think of any way that would simplify it any further.


EDIT:
If you solved this using the technique that others have suggested (involving the half-angle formula) you will arive at the exact same answer (after simplifying).

I personally like the way that I showed you better, though, because the half-angle formula is quite ugly (and I definitely don't have it memorized (because I never use it...)) and so I won't use it if there's a more simple way (by simple I mean that it only involves pythagorean's theorem)



P.S: in your attatchment, it would be good to also label the angle, θ (which is between OB and OA)

Also, feel free to ask questions if something I said didn't make sense (I know it's your first time with trig, and I tend to skip a lot of steps (out of habit) when I'm teaching people. You seem bright, though.)

 

[Govind_Balaji]

Imagine a circle of radius 1 (which they call the "unit circle," you'll learn all about it in trig.)
Sin(θ) is the y coordinate (a.k.a. the height of the leg) and cos(θ) is the x coordinate (a.k.a. the length of the other leg).
From the pythagorean theorem (since it's clearly a right triangle, and as I said, the radius (a.k.a. hypotenuse) is 1) you can derive the formula:
sin^{2}(θ)+cos^{2}(θ)=1 (you'll learn much about this as well)

Therefore you can simplify:
<br /> =r\sqrt{(\sin\theta)^2+1+(\cos\theta)^2-2\cos\theta}\\<br />
into:
<br /> =r\sqrt{2-2\cos\theta} = r\sqrt{2(1-\cos\theta)}\\<br />

There are various ways to rewrite cos(θ) (as you'll learn in trig.) but I can't think of any way that would simplify it any further.


EDIT:
If you did this using the technique that other's have suggested (involving the half-angle formula) you will arive at the exact same answer (once simplified).

I personally like the way that I showed you better, though, because the half-angle formula is quite ugly (and I definitely don't have it memorized (because I never use it...)) and so I won't use it if there's a more simple way (by simple I mean that it only involves pythagorean's theorem)

I don't understand even a single point of the half-angle formula as I am not familiar with trignometry. But I know Pythagoras theorem well and I can do it well.

I checked the formula $r\sqrt{2(1-\cos\theta)}$ with my original Problem. I got
$4sqrt{2(1-\cos\pi)}=4\sqrt{2(1-(-1))}=4\sqrt{4}=8m$

Thank you everybody very much. Can anyone clarify the half-angle stuff.

 

[Nathanael]

I checked the formula $r\sqrt{2(1-\cos\theta)}$ with my original Problem. I got
$4sqrt{2(1-\cos\pi)}=4\sqrt{2(1-(-1))}=4\sqrt{4}=8m$

It's pretty cool that you can now solve the same kind of problem with any two given times, isn't it? (assuming you can figure out the angle between the two times)
The problem that you originally asked (was it a school problem?) was the most simple that it could possibly be, but with a bit of trig you can now do any version of that problem :)

Thank you everybody very much. Can anyone clarify the half-angle stuff.

Don't even worry about the half-angle stuff!
Here's the gist of it:
There are some formulas called the "half angle formulas" that allow you to calculate the trigonemtric function of half of an angle in terms of the trig functions of the full angle. (It is NOT worth your time to memorize, seriously... I didn't even remember it, I just googled it. There's plenty of stuff to spend your time learning.)
Anyway, if instead of drawing a line straight down like I told you, you would draw a line that perfectly cuts θ in half (and it would also be perpendicular to AB in your picture). It would again create 2 right triangles, and it would be clear (from the picture) that sine of θ/2 is the half of the length you're trying to figure out (and it would be clear the radius is unchanged).

So you would take the half-angle sine formula and multiply the answer by 2, then simplify, and you'll get the same answer as you did with pythagoreans theorem.

I know I said don't worry about it and then went straight into detail about it (hahahah) but seriously... Don't bother memorizing the half-angle formulas, it will be a waste of time.

 

[Govind_Balaji]

was it a school problem?

Yes.

Don't even worry about the half-angle stuff!
Here's the gist of it:
There are some formulas called the "half angle formulas" that allow you to calculate the trigonemtric function of half of an angle in terms of the trig functions of the full angle. (It is NOT worth your time to memorize, seriously... I didn't even remember it, I just googled it. There's plenty of stuff to spend your time learning.)
Anyway, if instead of drawing a line straight down like I told you, you would draw a line that perfectly cuts θ in half (and it would also be perpendicular to AB in your picture). It would again create 2 right triangles, and it would be clear (from the picture) that sine of θ/2 is the half of the length you're trying to figure out (and it would be clear the radius is unchanged).

So you would take the half-angle sine formula and multiply the answer by 2, then simplify, and you'll get the same answer as you did with pythagoreans theorem.

I know I said don't worry about it and then went straight into detail about it (hahahah) but seriously... Don't bother memorizing the half-angle formulas, it will be a waste of time.

:thumbs: