You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Violation in diffraction? Lagrange (Optical) invariant
- Thread starter valeriy2222
- Start date
AI Thread Summary
The discussion revolves around the Lagrange invariant and its implications for radiance in optical systems. Participants clarify that while etendue can decrease, it cannot increase, emphasizing the conservation of optical throughput in lens systems. There is confusion between the concepts of radiance and etendue, with the latter being a geometrical property of the system, while radiance pertains to spatially extended emitters. The conversation highlights that focusing light into a smaller area requires an increase in the angle of radiance, but this must be done while maintaining the same light source and ideal focusing conditions. Ultimately, the participants stress the importance of understanding the relationship between radiance, etendue, and the physical constraints of optical systems.
Science news on Phys.org
mfb
Mentor
- 37,374
- 14,209
You cannot change it from left to right with a lense, but different setups can have different values of course.
valeriy2222
- 14
- 0
well, lagrange invariant says you can not.
- 7,670
- 3,719
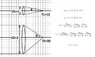
valeriy2222 said:It says you can not change with lenses the value L - radiance. Below I have an example where it proves that you can or where am I wrong? (I made L for 2D case, in 3D case everything the same - L2>L1)
I don't understand what you are trying to show. The optical invariant (or etendue) can be written a few different ways, but it is the product of aperture stop and numerical aperture of the system. The etendue can always decrease (for example, by stopping down a lens), but never increase- one way to show this is to calculate the determinant of the ABCD matrix of the optical system: for a thin lens, it equals 1, showing that etendue is conserved in this case. Are you trying to demonstrate something by connecting the two lenses into a beam concentrator/expander?
Perhaps you are confusing 'radiance' and 'etendue'- they are not the same thing. Etendue/optical throughput/optical invariant is a geometrical property of the system, while radiance is a property of spatially extended emitters.
mfb
Mentor
- 37,374
- 14,209
"Something is conserved/invariant" does not mean "this has the same value everywhere, for all setups".valeriy2222 said:well, lagrange invariant says you can not.
Energy is conserved, but a truck on a highway still has a larger energy than a snail moving across a road.
And I agree with Andy Resnick, I don't understand what your setups are supposed to show.
valeriy2222
- 14
- 0
Andy Resnick said:I don't understand what you are trying to show.
you focus some light (Watt) in a specific area (m2) and get a angle of radiance(sr - steradian). Then if you want at least the same amount of light into a smaller area the angle of radiance must increase. That's the Etendue/optical throughput/optical invariant. However, in the examples I have provided, I focus more light in the same area with the same angle thus breaking the L rule or what am I missing?
mfb
Mentor
- 37,374
- 14,209
If the light source is the same - it is not in your setups. And only if your focussing is ideal.valeriy2222 said:Then if you want at least the same amount of light into a smaller area the angle of radiance must increase.
Also, where is the area?
- 7,670
- 3,719
valeriy2222 said:you focus some light (Watt) in a specific area (m2) and get a angle of radiance(sr - steradian). Then if you want at least the same amount of light into a smaller area the angle of radiance must increase. That's the Etendue/optical throughput/optical invariant. However, in the examples I have provided, I focus more light in the same area with the same angle thus breaking the L rule or what am I missing?
I think you are mixing concepts- radiometry and ray optics, specifically. To be sure, a single 'ray' is associated with radiance, but if you are talking about collections of rays you have to be careful. For example, if a single ray enters through the entrance pupil and exits through the exit pupil, then the radiance is conserved (for that ray)- if there is vignetting, then the integrated radiance (luminous flux) is no longer conserved.
Ok- you have some luminous flux that passes through a lens: we should be talking in terms of irradiance (W/m^2) and intensity (W/sr). Then there's a second surface that the light is incident upon. Certainly, the irradiance incident on that second surface can be much higher than the irradiance of the initial optical field. However, say the second surface is underfilled by the incident light. You don't magically increase anything; in fact, if the second surface is a lens, you don't access the full optical power of the lens and can't focus the light down any further than you did previously.
Think of it this way- I have a microscope objective and fully illuminate the back aperture. Then, the light is focused down as normal- the spot size is (approximately) given by Abbe's formula. However, if I underfill the back aperture, the spot size is larger than Abbe's formula specifies because I don't access the full numerical aperture of the lens. In the limit that I illuminate the back aperture with a single ray, a single ray emerges from the lens and is not focused at all.
Does that help?
Similar threads
- Replies
- 7
- Views
- 2K
- Replies
- 1
- Views
- 2K
- Replies
- 20
- Views
- 2K
- Replies
- 12
- Views
- 3K
- Replies
- 12
- Views
- 341
- Replies
- 4
- Views
- 1K
- Replies
- 1
- Views
- 2K
- Replies
- 8
- Views
- 3K
- Replies
- 10
- Views
- 2K
- Replies
- 1
- Views
- 3K
Hot Threads
-
I Explain Bernoulli at the molecular level?
- Started by user079622
- Replies: 251
- Classical Physics
-
B Simple mass/scale puzzle
- Started by DaveC426913
- Replies: 206
- Classical Physics
-
I Is This....Right? Splitting LED colors is not working for me
- Started by Newtons Apple
- Replies: 40
- Optics
-
I Solving a momentum problem where masses change after the collision
- Started by rdemyan
- Replies: 35
- Classical Physics
-
B Torque Calculation - Not a basic application
- Started by TeeBeeCee
- Replies: 37
- Classical Physics
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 0
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 92
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math