- #1
bolbteppa
- 309
- 41
How do I visualize [itex]\dfrac{xdy-ydx}{x^2+y^2}[/itex]?
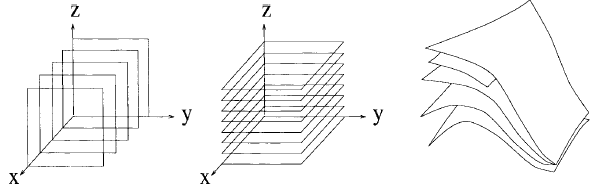
In other words, if I visualize a differential forms in terms of sheets:
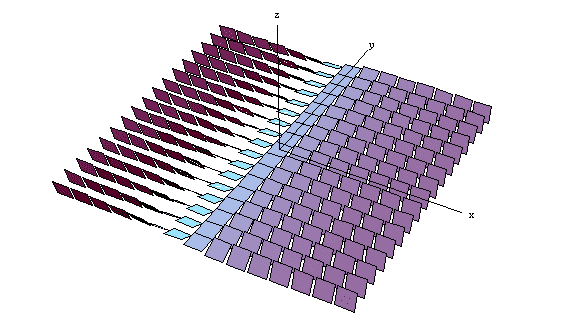
and am aware of the subtleties of this geometric interpretation as regards integrability (i.e. contact structures and the like):
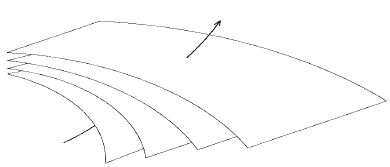
then since we can interpret a line integral as counting the number of sheets you cross through:
we see we can interpret the notion of a closed loop line integral as not being zero in terms of this contact structure idea, i.e. as you do the closed line integral you do something like enter a new field of sheets, what exactly are you doing & how does this explain the non-zero line integral around a closed loop at the origin for the differential form I've given above? Thanks!
In other words, if I visualize a differential forms in terms of sheets:
and am aware of the subtleties of this geometric interpretation as regards integrability (i.e. contact structures and the like):
then since we can interpret a line integral as counting the number of sheets you cross through:
we see we can interpret the notion of a closed loop line integral as not being zero in terms of this contact structure idea, i.e. as you do the closed line integral you do something like enter a new field of sheets, what exactly are you doing & how does this explain the non-zero line integral around a closed loop at the origin for the differential form I've given above? Thanks!