Voltage in capacitor after switch has been closed

[sailork]

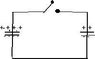
The drawing shows two fully charged capacitors (C1 = 2.00$$\mu$$F, q1 = 6.00$$\mu$$C; C2 = 8.00$$\mu$$F, q=12.0$$\mu$$C). The switch is closed, and charge flows until equilibrium is reestablished (i.e., until both capacitors have the sam voltage across their plates). Find the resulting voltage across either capacitor.

**i have attached a jpg of the drawing

Homework Equations

q=CV , 1/Cs=1/C1+1/C2

The Attempt at a Solution

I know the capacitors are in series so I have attempted to find the resultant capacitance, as well as working from the voltages calculated via q=CV. However, I have been unable to find the answer listed in the back o the text (1.80 V). Please help point me in the correct direction.

 

[Redbelly98]

Welcome to PF

As a rule of thumb, series capacitors have the same charge, while parallel capacitors have the same voltage. Which is the case here?

 

[sailork]

Well by what is given in the problem, we are looking for the two capacitors to have the same voltage across their plates, but according to the drawing, the appear to be in series. However, if you look at the two capacitors as if they were in parallel, it would give the answer that is found in the back of the book. Is there a reason that they would be in parallel even though the image makes them appear to be in series?

 

[Jasso]

Think of it this way:

Where would you put the voltage probes to measure the voltage?

What would the circuit diagram look like?

 

[willem2]

This is the one case where two capacitors are both in series and parallel (after the switch closed)

you get much further by considering them as parallel however, because:

Series capacitors have the same charge but only if they start out with the same charge. This is not the case here.
you can replace 2 series capacitors with their equivalent and it won't make a difference to the rest of the circuit, but this won't allow you to say anything about the charges of the 2 separate capacitors.

Parallel capacitors always have the same voltage across them. No ifs or buts here.
If you replace 2 parallel capacitors with their equivalent, the equivalent capacitor will have the same voltage across it as the original 2, making it easy to find out the charges on the original capacitors if you know the voltage across the equivalent capacitor.