Voltage vs Time Homework: Solve for Approx. Volts

[J89]

Homework Statement

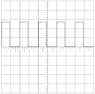
Your lab partner is opening and closing the tap switch to turn on and off the voltage from a battery. If you see the following trace on the screen and the VOLTS/DIV knob is set to 0.5 V and the TIME/DIV dial is set to 2s/DIV, you can tell that the voltage of the battery is approximately how many volts?

Homework Equations

No known equations that I know of...

The Attempt at a Solution

Well we know that the y-axis is all together .5 volts, and the x-axis is 2 seconds..so it would common to just multiply .5 by 2..however, it's not one of the choices. So I thought that in the graph since there are three tick marks, you would divide .5/3 and 2/3 and then multiply that together..still did not get it correct..I don't know what I am doing wrong, that was how I was shown it was done.

 

[Borek]

Well we know that the y-axis is all together .5 volts, and the x-axis is 2 seconds..so it would common to just multiply .5 by 2.

Time scale is unrelated to the problem.

So I thought that in the graph since there are three tick marks, you would divide .5/3 and 2/3 and then multiply that together..still did not get it correct..I don't know what I am doing wrong, that was how I was shown it was done.

Your signal seems to be almost three ticks high, doesn't it? And there is 0.5V per tick, yes?

That's not different from using a ruler to measure something.