Washer Hanging from Box Moving Down a Ramp

[Gwozdzilla]

Homework Statement

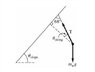
A steel washer is suspended inside an empty shipping crate from a light string attached to th top of the crate. The crate slides down a long ramp that is inclined at an angle of 37° above the horizontal. The crate has mass 180kg. You are sitting inside (with a flashlight); your mass is 55kg. As the crate is sliding down the ramp, you find the washer is at rest with respect to the crate hen the string makes an angle of 68° with the top of the crate. What is the oefficient of kinetic friction between the ramp and the crate?

Homework Equations

ƩF=ma
f_k=μn

The Attempt at a Solution

Let m_c = mass of crate
and m_y = mass of you
and m = mass of washer
ƩF_{crate system} = (m_c + m_y)a = (m_c + m_y)gsin(37) - μ(m_c + m_y)cos(37)

Canceling out the combined mass and solving for μ gives:

μ = [gsin(37) - a]/[gcos(37)]

Apparently...
Let T = tension in string
ƩF_y-washer = ma₁ = Tsin(22) -mgsin(37)
and
ƩF_x-washer = ma₂ = Tcos(22) -mgcos(37)

And a₂ = 0 allowing for these two equations to be rearranged and then divided by each other giving...
tan(22) = [gsin(37) - a]/[gcos(37)]

My actual question:

Where are the ƩF_washer equations coming from? I have the attached picture to help, but I still don't understand.

 

[Simon Bridge]

Where are the ƩF_washer equations coming from? I have the attached picture to help, but I still don't understand.

Free body diagram for the washer.
So you didn't derive the equations yourself then?

You can also look at it from the POV of you - if the crate were stationary on the slope, what angle would the washer make to the ceiling?