Water and Gravity: Can Water Lift Weights?

[Idea04]

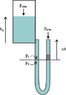
I'm stuck on a problem. I know that for 1 psi you need 2.31 feet of water in a column. But I don't believe that water form a tube 1" diameter and 7' tall, (.4870838 pounds of water equals 6.201psi) could lift a weight. My problem is let's say there is a horizontal cylinder tank suspended 7' above ground.
And it had a tube attacked to it going down to the ground 7' and then back up 7'. But on the way up it encountered a 25 or 20 pound weight.
Now the weight of the water verticle in the tube weighs less than the weights. So I know the water will stop in that case. But if the tank is full of water will the gravitational flow of water push the weights up. Even though the pressure would only be the static pressure from the verticle tube.

 

[Doc Al]

I'm not quite sure what the exact problem is, but the static force that the water can exert depends only on the water pressure and the area of the tube. The pressure, in turn, depends only on the depth of the water, not how much water is in the tank.

In other words: If the distance between the water surface in the tank to the bottom of the tube is 7 feet, then the pressure at the bottom of the tube is that due to 7 feet of water (not counting atmospheric pressure).

 

[Idea04]

Would the flow of the water moving out of the tank at the acceleration of gravity create enough force to push the weight upwards.

 

[andrevdh]

Lets assume that the pressure of the weight, p_w, is sufficient to prevent the fluid from flowing. The pressure at point 1 and 2 need to be the same:
p_{atm}+\rho gh_t+p_{\Delta h} = p_{atm}+p_{\Delta h}+p_w
which gives
\rho gh_t=p_w
or
h_t=\frac{W}{\rho gA}
where W is the weight of the mass in the pipe with a cross sectional area A. Since the weight is surrounded by water one should include the buoyancy B by subsituting W with W-B in the equation above.
If the head of the water in the tank is greater than this it should result in a flow.

 

[Idea04]

thanks so if I get this right the weight divided by the area is the pressure and if the pressure of the water is greater than the weight then there will be flow. So even in the situation that the weight was wider in diameter it would still result in flow because of pounds per square inch. The weight would have a lower pressure value than the water.
But for another question how do you calculate the pressure difference when water from a pipe flowing downward by gravity, starts flowing upward through a larger pipe. What would be the upward force?

 

[andrevdh]

In order to get some sort of idea of what one can expect I have made many assumptions to get to the basic equation. Like for instance the mass is acting like a piston in a cylinder, that is the water cannot slip past it on the sides. The basic equation states that the pressure at the bottom of the water tank (excluding atmospheric pressure) weighs up against the pressure exerted by the mass (its weight divided by its cross sectional area). The direction of flow will be controlled by which ever pressure is bigger.

The flow in the system is regulated by pressure differences in the system. The diameter of the pipe will not influence these differences. What one get in a u-type of system is that the pressure in the one arm needs to be larger than that in the other arm in order to effect a flow out of the system. This is achieved by the head in the tank (water reservoir), which normally is build with a large diameter in order to cope with any outflow. The drop in the level in a large diameter tank will therefore be small which means it will effectively maintain is pressure.