Compressed air Pushing a Column of Water

[Ironwood]

TL;DR Summary

How much compressed air will it take to push a given volume of water up a given height at a certain rate?

Greeting,

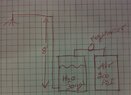
I have been noodling on this problem for a bit and was hoping to have some input from this form. what volume of compressed air, at 200 PSI, will it take to push lets say 30 gallons of water 8 feet up a 3/4" pipe at a minimum of 8 gpm with a minimum pressure of 8psi at the top if there is a regulated pressure between the two tanks? so imagine an air tank with a pipe running from it to the top of a pressure rated water tank, and from the water tank a pipe running from the bottom up 8 feet. How much air, volumetrically, will there need to be in the first tank to push all 30 gallons up the pipe at the minimum pressure and not run out of air by the end. and also how long will it take?

 

[russ_watters]

You can do a first approximation with the ideal gas law. I get about half a cubic foot. But:

• The compressed air will cool, so you'll need more. That can be calculated but it is more involved.
• How long is mostly a function of pipe size.
• Water remaining in the pipe may be significant for larger pipe sizes.

 

[Lnewqban]

Welcome, @Ironwood !

Could you show us a diagram of your set up?
I can't see the thing clearly in my mind.

How can your injection of compressed air achieve a steady flow of "30 gallons of water 8 feet up a 3/4" pipe at a minimum of 8 gpm"?

Also, do you need to calculate the volume of air at 200 psi or at the pressure inside the water tank?

 

[russ_watters]

Some additional notes:

• You specified 3/4" pipe but I don't know if that's just outlet size or all of it.
• Maximum flow rate is highly dependent on exqct configuration.
• I assume a regulator will be needed to provide constant outlet pressure and/or flow.
• "Outlet pressure" is only a thing if dumping into another pressurized tank. Otherwise it's atmospheric.

 

[Ironwood]

Welcome, @Ironwood !

Could you show us a diagram of your set up?
I can't see the thing clearly in my mind.

How can your injection of compressed air achieve a steady flow of "30 gallons of water 8 feet up a 3/4" pipe at a minimum of 8 gpm"?

Also, do you need to calculate the volume of air at 200 psi or at the pressure inside the water tank?

I would love to show you the idea, I'll see if I can attach a photo. yes the volume of air at 200 psi,

 

[Ironwood]

Some additional notes:

• You specified 3/4" pipe but I don't know if that's just outlet size or all of it.
• Maximum flow rate is highly dependent on exqct configuration.
• I assume a regulator will be needed to provide constant outlet pressure and/or flow.
• "Outlet pressure" is only a thing if dumping into another pressurized tank. Otherwise it's atmospheric.

- for the pipe, there is a range but I specified 3/4" because that is in the middle of the range. there is a nozzle on the end of the outlet pipe as well, and a regulator in between the air and water tanks.
-I'll attach a quick drawing of the configuration, feel free to ask for more details.
-yes, I dont want all the air to dump into the water tank at once I want a steady output and so a regulator is what I was considering.

-the outlet pressure is indeed atmospheric, but there is a nozzle on the end of the outlet pipe that will output 8 gpm at 7.11 psi, that is why I specified that.

 

[Ironwood]

I feel like Bernoulli's principal and the ideal gas law is where I should start, but as the pressure goes down in the air tank and the volume increases in the water tank I am not sure how to calculate the change.

 

[Ironwood]

You can do a first approximation with the ideal gas law. I get about half a cubic foot. But:

• The compressed air will cool, so you'll need more. That can be calculated but it is more involved.
• How long is mostly a function of pipe size.
• Water remaining in the pipe may be significant for larger pipe sizes.

so almost four gallons of air at 200 psi is all it would take to move 30 gallons up 8 feet?

 

[Lnewqban]

I would love to show you the idea, I'll see if I can attach a photo. yes the volume of air at 200 psi,

It looks like a tank feeding a shower.
In that case, the first safety thing that you need to specify is a pressure relief valve for your water tank.
The reason is that the regulator may fail, over-pressurizing a tank that could explode and hurt people and property nearby.

In order to get a marginal flow of water out of the shower, the air static pressure above the water in the tank, when its level is the lowest should be equivalent to 8-foot column of water.

At least in the U.S., a typical home's water pressure should be somewhere between 45 to 55 psi, while shower heads are limited to a maximum flow of around 2.5 gallons per minute.

If we want a more practical flow, we should increase that pressure via the regulator.
About 50 psi above atmospheric pressure should do it.

Regarding volume of air at that pressure, you could do an estimate based on the Boyle's law.

Please, see:
https://www.engineeringtoolbox.com/compressed-air-storage-volume-d_843.html

https://www.engineeringtoolbox.com/hydrostatic-pressure-water-d_1632.html

 

[Ironwood]

It looks like a tank feeding a shower.
In that case, the first safety thing that you need to specify is a pressure relief valve for your water tank.
The reason is that the regulator may fail, over-pressurizing a tank that could explode and hurt people and property nearby.

In order to get a marginal flow of water out of the shower, the air static pressure above the water in the tank, when its level is the lowest should be equivalent to 8-foot column of water.

At least in the U.S., a typical home's water pressure should be somewhere between 45 to 55 psi, while shower heads are limited to a maximum flow of around 2.5 gallons per minute.

If we want a more practical flow, we should increase that pressure via the regulator.
About 50 psi above atmospheric pressure should do it.

Regarding volume of air at that pressure, you could do an estimate based on the Boyle's law.

Please, see:
https://www.engineeringtoolbox.com/compressed-air-storage-volume-d_843.html

https://www.engineeringtoolbox.com/hydrostatic-pressure-water-d_1632.html

I appreciate the engineering feedback, you're close on the application. This is actually a fire suppression system for an off-grid application with no access to consistent power or water. I want the thing to sit there charged and ready to go to be triggered at a moment's notice, I've already specked pressure release valves for both the air and the water tanks. I specified 8.0 PSI because that was the minimum pressure allowed for adequate operation at 7 gallons per minute on the water suppression sprinkler. I'm aiming for the low end of what is allowable because it will be a static volume of water in the tank and I would like to reduce the overall volume as much as possible while still allowing for an adequate amount of time under spray.

 

[erobz]

I appreciate the engineering feedback, you're close on the application. This is actually a fire suppression system for an off-grid application with no access to consistent power or water. I want the thing to sit there charged and ready to go to be triggered at a moment's notice, I've already specked pressure release valves for both the air and the water tanks. I specified 8.0 PSI because that was the minimum pressure allowed for adequate operation at 7 gallons per minute on the water suppression sprinkler. I'm aiming for the low end of what is allowable because it will be a static volume of water in the tank and I would like to reduce the overall volume as much as possible while still allowing for an adequate amount of time under spray.

Since the flow is being constrained to be steady by controlling the pressure in the tank we can use the Energy Equation from fluid mechanics ( not exactly Bernoulli's, but close). You will find that the for the flow to be steady (flow velocities change only in position, not time), the absolute pressure in the water tank should decrease linearly with the height of water $z$ remaining in the tank at time $t$. How you are going to do that is your challenge.

If you are interested in the how the energy equation is applied:

$$ \frac{P(z)}{\rho g} + z + \alpha \frac{V^2_{tank}}{2g} = \frac{P_{atm}}{\rho g} + H + \alpha \frac{V^2_{exit}}{2g} + \sum_{{tank} \to {exit}} \frac{k_i L_i}{D_i} \frac{V_i^2}{2g} $$

 

[russ_watters]

so almost four gallons of air at 200 psi is all it would take to move 30 gallons up 8 feet?

I started with the end state which is 8 psi at the nozzle plus atmospheric pressure plus 3.5 psi of head (elevation) for a total of about 26 psi. That's what the air tank has to finish with. From Boyle's law (derived from the ideal gas law), the pressure ratio is the inverse of the volume ratio: 30 gal moved * 26/215 = 3.6 gal.

Again, this doesn't account for how the compressed air will cool as it expands.

Another limitation is that the piping system will have some pressure loss, which you'd need to calculate by adding-up the losses of all the elements (straight runs and fittings/elbows) in the system. I'm thinking this will be fairly small at the specified flow and 3/4" pipe size, but you didn't provide piping lengths and I know that's just a vague diagram, so that may not be true.