Water level in a submerged closed vessel after it is turned upright

[vepexu]

TL;DR

Closed pipe at the sea floor is filled with water and air inside is compressed. After pipe is raised to surface. What is the water level inside the pipe?

Hello all,

I need Your help with one real / theoretical situation.

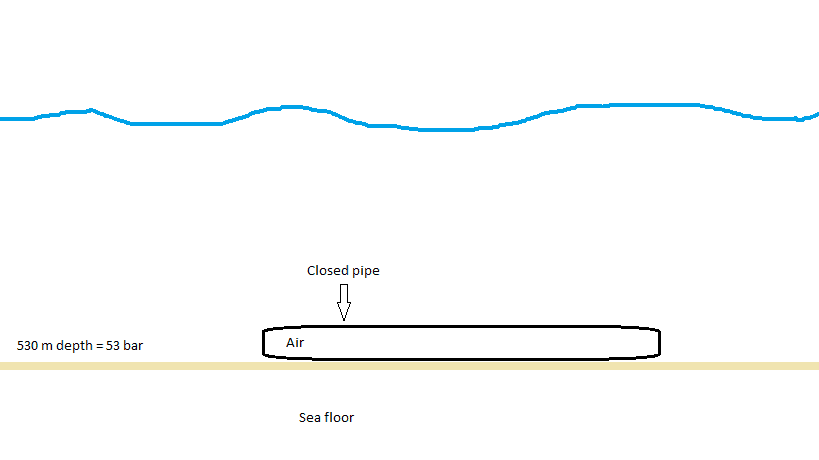
We have submerged pipe filled with air at atmospheric pressure that is closed on both ends.

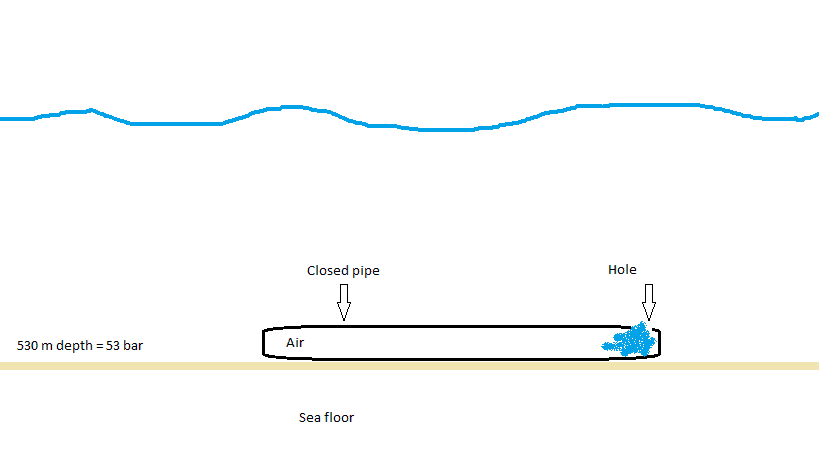
The hole is formed on one pipeline end and the water starts flooding the pipe.

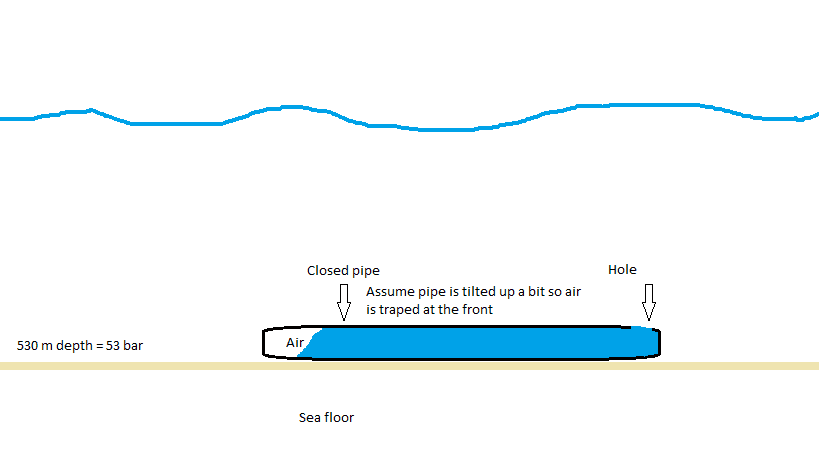
Let's assume pipe is tilted somewhat and that no air escaped from the pipe.
Now we have flooded pipe with whole pipe volume of air compressed to 53 bar at the front.

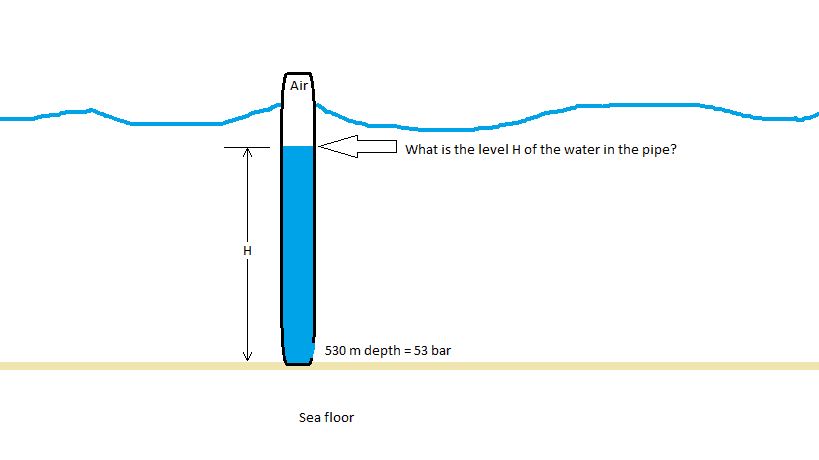
Now we recover the pipe end to the surface, we can assume vertically, but it is in an arch with top section completely vertical.
What is the level H of the water in the pipe?

 

[berkeman]

Seems pretty straightforward. Can you show us your attempt at the calculation?

 

[vepexu]

I used p1V1 = p2V2 to calculate the volume of the compressed air when the pipe is laid at the bottom.
But when the pipe is turned vertical we need to take into account the height of the water column in the pipe. At what pressure there will be equilibrium between water level and air inside and what equation to use is where I'm stuck.

Edit:
And we can also assume the pipe end is maybe 1 m above water surface so we can say it is in line with surface of the water if it makes things easier.

 

[berkeman]

Remember that for most calculation purposes, water is incompressible. Does that help?

 

[vepexu]

Yes, but, my calculation was for air when the pipe was laid down. So if we have for example 106 m³ volume of air in pipe (same as pipe inner volume). When the water rushes in at 53 barG (we assume non of the air escaped) air will be compressed to volume of:

1 bar x 106 m³ = 53 bar x V₂ ====> V₂ = 2 m³ of air ====> Volume of water is then 104 m³

I don't know exactly what will happen when we turn it vertical as per image in my first post. At which water level H in the pipe will there be an equilibrium between trapped air and water. Since in this position we have water column as well. If the pipe were to be opened at the top air would be vented and the H will be at the same level as water surface, but since this is a closed pipe we still have 106 m³ of air trapped at the top and water column above the hole at the bottom where a pressure of 53 barG is applied.

 

[Baluncore]

Assume the pipe is 530 m long and of constant section.
Assume the opening in the pipeline remains 530 m down at 53 bar hydrostatic pressure.
If you lift the air end to touch the surface you will have internal air pressure opposing the hydrostatic pressure of the water at the depth h, where it will be ( 10 * h h/10 ) bar.
P1⋅V1 = P2⋅V2 ;
1 bar * 530 m = (10 * h / 10 ) * h ;
h² = 53 ; 5300
h = 7.28 m. 72.8 m.
But can you believe it ? Corrected.

 

[256bits]

Assume the pipe is 530 m long and of constant section.
Assume the opening in the pipeline remains 530 m down at 53 bar hydrostatic pressure.
If you lift the air end to touch the surface you will have internal air pressure opposing the hydrostatic pressure of the water at the depth h, where it will be ( 10 * h ) bar.
P1⋅V1 = P2⋅V2 ;
1 bar * 530 m = (10 * h) * h ;
h² = 53 ;
h = 7.28 m.
But can you believe it ?

from the top surface?

 

[gmax137]

@Baluncore (I'm reluctant to say this to you, but) check your units; I get 74 meters from the top surface. I think you dropped a factor of ten somewhere.

 

[gmax137]

hydrostatic pressure of the water at the depth h, where it will be ( 10 * h ) bar.

I think this should be (h/10) bar.

$P = h \rho g = h*1000* 10 \frac{m*kg*m*bar}{m^3*sec^2*100,000pascal} = \frac h {10}$

here, this is clearer:
$\frac{m}{} \frac{kg}{m^3} \frac{m}{sec^2} \frac{bar}{100,000pascal}$

 

[256bits]

At which water level H in the pipe will there be an equilibrium between trapped air and water. Since in this position we have water column as well.

You do realize that your situation is the same as if the pipe filled with atmospheric air is lowered into the water.
Solve for the rise of water level into the pipe.
As per previous posts.

 

[Baluncore]

(I'm reluctant to say this to you, but) check your units; I get 74 meters from the top surface. I think you dropped a factor of ten somewhere.

You are correct. I multiplied by 10, instead of dividing by 10.
Then the square root reduced my error by a factor of 10.

But can you believe it ?

It didn't seem right. You shouldn't believe it, you didn't.
Thanks for finding my error.

It is a most interesting problem.

 

[vepexu]

So at the end of the day we have 73 m section with air at @ 7,16 bar and 457 m section with water column at 45,7 bar.
It is important to know air pressure at the top when the pipe is about to be vented.

 

[Baluncore]

I over-simplified the solution by fixing the length of the pipe so it would be vertical when lifted.
But the length of the pipe is critical to the solution because it decides the mass of air involved.
I also used gauge pressure, not absolute pressure in the Boyle's law ratio.

Here is a more general solution that requires the length of the pipeline be specified. Only the part of the pipe that contains air is assumed to be vertical. The higher closed end is assumed to be at the surface. The pipe is assumed to have a constant section, so volume will be proportional to length. The position of the water filled part of the pipe, and the pressure at the hole, is irrelevant as the hydrostatic pressure inside and outside the pipe will cancel.
I ignore water temperature density differences and the hydrostatic pressure in the air column.

The total length of pipe is, s; metre.
The length of the upper part containing air is, d; metre.
I assume hydrostatic pressure gradient is 1 bar per 10 metre in sea water.
The gauge pressure of air in the pipe is, Pg = d / 10; bar.
The absolute pressure in the pipe is, p = ( d / 10 ) + 1; bar.
Boyle's law uses absolute pressure. P1·V1 = P2·V2;
Therefore, 1 * s = p * d;
0 = ( d² / 10 ) + d – s
d = 5 * ( √( 1 + 0.4 * s ) − 1 ); I believe this is the correct quadratic solution.

Example results:
s = 1 m; d = 0.916 m. You can test this in a pool.
s = 5 m; d = 3.660 m.
s = 20 m; d = 10.00 m. This special test case appears correct.
s = 50 m; d = 17.91 m.
s = 150 m; d = 34.05 m.
s = 530 m; d = 67.97 m.
s =1060 m; d = 98.07 m.

When s = 530 m, d = 67.97, the absolute air pressure is 6.797 bar.
The gauge pressure of air in the pipe at the surface is 5.797 bar.

 

[Baluncore]

When s = 530 m, d = 67.97, the absolute air pressure is 6.797 bar.
The gauge pressure of air in the pipe at the surface is 5.797 bar.

Did I get it wrong again ?
When s = 530 m, d = 67.97 m, the gauge air pressure is 6.797 bar ≈ 99 psi if vented.
The absolute pressure of air in the pipe will then be 7.797 bar.

 

[gmax137]

Did I get it wrong again ?
When s = 530 m, d = 67.97 m, the gauge air pressure is 6.797 bar ≈ 99 psi if vented.
The absolute pressure of air in the pipe will then be 7.797 bar.

That's pretty close to what I got. I solved in US units; converted to SI I get 69.0 meters air space at 7.78 bar absolute (6.77 barg or 98.2 psig). I think the differences might be due to your use of 10 m/sec^2 vs. 9.8 for gravity. That was perfectly reasonable the first time thru but once you develop the quadratic to solve the problem you might as well use a more refined value, IMO.

So at the end of the day we have ... 457 m section with water column at 45,7 bar.

This is a little ambiguous but I think it shows the OP doesn't understand the solution.

 

[Baluncore]

I think the differences might be due to your use of 10 m/sec^2 vs. 9.8 for gravity. That was perfectly reasonable the first time thru but once you develop the quadratic to solve the problem you might as well use a more refined value, IMO.

If you select g = 9.8 you should also accept the density of seawater to be 1.025 kg/L.
9.8 *1.025 = 10.045 so 10.0 ±0.5% is close enough for unspecified temperature and salinity.

This is a little ambiguous but I think it shows the OP doesn't understand the solution.

I did not understand the problem, or the irrelevance of the depth, until my first attempt was corrected. Someone may find this thread one day and benefit.