PFuser1232
- 479
- 20
Homework Statement
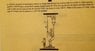
A former student of mechanics wishes to weigh himself but has access only to a scale A with capacity limited to 400 N and a small 80 N spring dynamometer B. With the rig shown he discovers that when he exerts a pull on the rope so that B registers 76 N, the scale A reads 268 N. What is his mass ##m##? Also, what range of weight could be measured by this system?
Homework Equations
Since the student is in equilibrium:
$$\sum F_y = 0$$
The Attempt at a Solution
The normal reaction acting on the student is 268 N. There are two tensions acting on the student; ##T_1## and ##T_2## (see diagram).
##T_1## is clearly 76 N. However, I can't seem to find ##T_2##. How do I assign a value to ##T_2## based on the arrangement of the ropes shown in the diagram?
Once found:
$$m = \frac{T_1 + T_2 + N_A}{g}$$
Update: I tried finding ##T_2## by first noting that the tension throughout the string from B to the ceiling is 76 N. Applying the equilibrium condition for the two pulleys with strings directly attached to the triangular support to which the rope in question is attached. We now have ##T_2 = 4T_1##.
Is this correct?
Attachments
Last edited: