Weight held by a beam and cable

In summary, the conversation discusses a problem involving a weight being held to the side of a building using a beam and a cable. The weight is 336 pounds and the angle between the cable and beam is 49 degrees. The goal is to calculate the tension of the cable and the force of the beam. The force of gravity is calculated to be 3292.8 lbf. However, there is confusion about why the weight is being multiplied by the acceleration due to gravity. The correct answer for the force of the beam is 2862.4 lbf.
  • #1
EchoTheCat
21
1
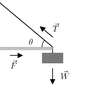
I've got a problem where a weight is being held to the side of a building using a beam and a cable. The weight is 336 pounds and the angle between the cable and the beam is 49 degrees. I need to calculate the tension of the cable and the force of the beam. I calculated the force of gravity as being 336*9.8 = 3292.8 lbf. If the tension in the cable is T, then sin 49 degrees = 3292.8 / T. I solved for T to be 4363.0027845 lbf. I calculated the force of the beam to be 3292.8/tan 49 degrees = 2862.4 lbf, but that's not the correct answer. I don't know what I've done wrong?
 

Attachments

  • tension..PNG
    tension..PNG
    1.1 KB · Views: 397
Physics news on Phys.org
  • #2
The objects weight is already given in force units, not mass units. Why are you multiplying it by g? The weight of any object is always in force units in USA or SI systems of measure.
 
  • #3
You're right. Thank you!
 

What is weight held by a beam and cable?

The weight held by a beam and cable refers to the amount of force that can be supported by a beam and cable system without breaking or failing. This is an important consideration in engineering and construction, where beams and cables are often used to support heavy loads.

What factors affect the weight held by a beam and cable?

The weight held by a beam and cable is influenced by several factors, including the material and size of the beam and cable, the angle and direction of the force being applied, and the condition and strength of the supporting structures.

How is the weight held by a beam and cable calculated?

The weight held by a beam and cable is typically calculated using mathematical equations that take into account the properties of the materials, the geometry of the beam and cable, and the applied load. These calculations are important for ensuring the safety and stability of the structure.

What is the maximum weight that can be held by a beam and cable?

The maximum weight that can be held by a beam and cable varies depending on the specific design and construction of the system. However, engineers typically use safety factors and load limits to ensure that the weight held by a beam and cable does not exceed its capacity.

What happens if the weight held by a beam and cable exceeds its capacity?

If the weight held by a beam and cable exceeds its capacity, the beam and cable may fail, leading to structural damage or collapse. This is why it is important to carefully calculate and consider the weight held by a beam and cable in any construction or engineering project.

Similar threads

Seemingly simple equilibrium problem - force balance
    • Introductory Physics Homework Help
Replies
6
Views
1K
Does distance affect torque in hanging sign problem?
    • Introductory Physics Homework Help
2
Replies
42
Views
2K
Problem involving space elevators
    • Introductory Physics Homework Help
Replies
19
Views
808
Tension and net torque in a cable
    • Introductory Physics Homework Help
Replies
10
Views
4K
Finding the tension of two cables holding an object at rest
    • Introductory Physics Homework Help
Replies
7
Views
2K
Solve Static Equilibrium: Beam, 520N Force, Cable Tension
    • Introductory Physics Homework Help
Replies
2
Views
1K
Torque and Rotational Equilibrium with a slanted Rod/Cable
    • Introductory Physics Homework Help
Replies
7
Views
2K
Equilibrium : normal reaction of a rotational center?
    • Introductory Physics Homework Help
Replies
2
Views
985
Confusion about type and quantity of force being exerted
    • Introductory Physics Homework Help
Replies
2
Views
3K
What is the torque on the bolt due to the worker and the weight of the beam?
    • Introductory Physics Homework Help
Replies
1
Views
2K

Hot Threads

Recent Insights

Back
Top