xseven
- 2
- 0
Hi!
I am trying to build a stand with a boom arm for my acting classes and I need to find the weight required to balance it. The problem is that it looks like I was more like a swan when I was swimming in the physics lessons ... no a lot of drops stayed on my plumage ... :)
Help?!
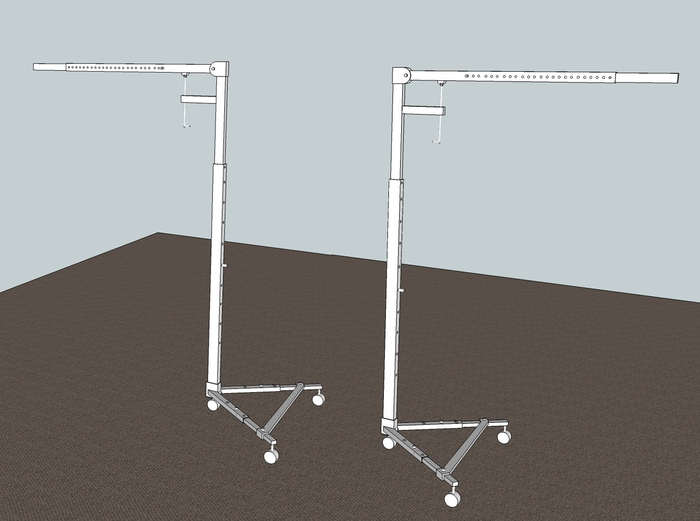
Data:
Stand height: "H" (more or less 2 m fully extended)
Boom arm: "B" (again, more or less 2 m fully extended) - the arm can be lifted rotating a threaded rod so I assume the length of the boom is (for the purpose of a formula) a+b (where "a" will be between the hinge and the rod's point of contact)
Legs: "L"
The questions that are troubling me are as follows:
1. What is the most stable configuration of legs? an angle of 90°? 60°?
2. What formula can calculate the weight required to stabilize the system when weight "W" (more or less 10 KG) is attached to the boom arm fully extended pointing away from the legs?
3. What formula can calculate the weight required to stabilize the system when weight "W" is attached to the boom arm fully extended pointing in the same direction with the legs?
... And 4 (already feeling that I push the limits of your patience) ... I would like the threaded rod to be as short and as close as possible to the main pole - is there a way to calculate the force required to raise the boom arm with the weight to a 45° angle from the horizontal position? How close to the stand can I put it and still manage to have a smooth rotating action?
Humbly yours,
Cat
I am trying to build a stand with a boom arm for my acting classes and I need to find the weight required to balance it. The problem is that it looks like I was more like a swan when I was swimming in the physics lessons ... no a lot of drops stayed on my plumage ... :)
Help?!
Data:
Stand height: "H" (more or less 2 m fully extended)
Boom arm: "B" (again, more or less 2 m fully extended) - the arm can be lifted rotating a threaded rod so I assume the length of the boom is (for the purpose of a formula) a+b (where "a" will be between the hinge and the rod's point of contact)
Legs: "L"
The questions that are troubling me are as follows:
1. What is the most stable configuration of legs? an angle of 90°? 60°?
2. What formula can calculate the weight required to stabilize the system when weight "W" (more or less 10 KG) is attached to the boom arm fully extended pointing away from the legs?
3. What formula can calculate the weight required to stabilize the system when weight "W" is attached to the boom arm fully extended pointing in the same direction with the legs?
... And 4 (already feeling that I push the limits of your patience) ... I would like the threaded rod to be as short and as close as possible to the main pole - is there a way to calculate the force required to raise the boom arm with the weight to a 45° angle from the horizontal position? How close to the stand can I put it and still manage to have a smooth rotating action?
Humbly yours,
Cat