Engineering Weird looking circuit -- Can someone check my attempt?

[eehelp150]

Homework Statement

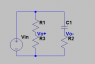
This is kind of what the circuit looks like:

Homework Equations

KCL

The Attempt at a Solution

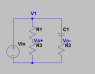
This my attempt at "normalizing" it:

Solving Attempt:
$\frac{V_{in}-V_o}{R_1}+C_1\dot{V_{in}}=0$
$\frac{V_o-V_{in}}{R_1}+\frac{V_o}{R_3+R_2}=0$

Are my equations correct?

 

[cnh1995]

Are my equations correct

No. The output voltage does not involve ground (-ve terminal of Vin). Hence, V_o=Vο⁺-Vo^-. You need to use both Vo⁺ and Vo^- in the KCL equation.
Also, voltage across the capacitor is not Vin as you have taken in the first equation.

What exactly is the question asking for?

 

[eehelp150]

No. The output voltage does not involve ground (-ve terminal of Vin). Hence, V_o=Vο⁺-Vo^-. You need to use both Vo⁺ and Vo^- in the KCL equation.
Also, voltage across the capacitor is not Vin as you have taken in the first equation.

What exactly is the question asking for?

Sorry, I thought I wrote it out. The prompt is "Find the differential equation for Vo"
node vo+ (Vo+ = Vop, Vo- = Vom)
$\frac{V_{op}-V_{in}}{R_1} + \frac{V_{op}-V_{om}}{R_3+R_2}=0$

$C_1(\dot{V_{om}}-\dot{V_{in}}) + \frac{V_{om}-V_{op}}{R_2+R_3}=0$

 

[cnh1995]

Sorry, I thought I wrote it out. The prompt is "Find the differential equation for Vo"
node vo+ (Vo+ = Vop, Vo- = Vom)
$\frac{V_{op}-V_{in}}{R_1} + \frac{V_{op}-V_{om}}{R_3+R_2}=0$

$C_1(\dot{V_{om}}-\dot{V_{in}}) + \frac{V_{om}-V_{op}}{R_2+R_3}=0$

I didn't follow your equations. Basically, the currents do not add to zero. You are taking only two currents out of three. I think KCL method is not useful here.

 

[eehelp150]

I didn't follow your equations. Basically, the currents do not add to zero. You are taking only two currents out of three. I think KCL method is not useful here.

Is this better?
Vo+ = V1
Vo- = V2

$\frac{V_{in}-V_1}{R_1} + C_1(\dot{V_{in}}-\dot{V_{2}})=0$

$\frac{V_1}{R_3}+\frac{V_1-V_{in}}{R_1}=0$

$\frac{V_2}{R_2}+C_1(\dot{V_2}-\dot{V_{in}})=0$

 

[cnh1995]

Is this better?
Vo+ = V1
Vo- = V2
View attachment 109594

View attachment 109595
$\frac{V_{in}-V_1}{R_1} + C_1(\dot{V_{in}}-\dot{V_{2}})=0$

View attachment 109596
$\frac{V_1}{R_3}+\frac{V_1-V_{in}}{R_1}=0$

View attachment 109597
$\frac{V_2}{R_2}+C_1(\dot{V_2}-\dot{V_{in}})=0$

Basically, the currents do not add to zero. You are taking only two currents out of three. I think KCL method is not useful here.

The currents do not add to zero. I believe you need to use a different method. I'll get back to you on this later.

 

[eehelp150]

The currents do not add to zero. I believe you need to use a different method. I'll get back to you on this later.

Is nodal analysis doable or do I need to use meshcurrent?

 

[gneill]

Nodal analysis is doable, you just have to recognize how to apply it. It might help if you were to forget +Vo and -Vo labels for a moment and replace them with V1 and V2 (Hence Vo = V1 - V2). Find V1 and V2 separately.

 

[eehelp150]

Nodal analysis is doable, you just have to recognize how to apply it. It might help if you were to forget +Vo and -Vo labels for a moment and replace them with V1 and V2 (Hence Vo = V1 - V2). Find V1 and V2 separately.

$\frac{V_{in}-V_1}{R_1} + C_1(\dot{V_{in}}-\dot{V_2}) = 0$
$\frac{V_1-V_{in}}{R_1}+\frac{V_1}{R_3}=0$
$\frac{V_2}{R_2}+C_1(\dot{V_2}-\dot{V_{in}})$
What is wrong with my equations?

 

[gneill]

The first one is not a node equation. Vin is not an essential node, it is part of the reference supernode since it has a fixed potential with respect to the reference node.

The second equation is good. Solve it for V1.

The third equation is also good. Solve it for V2.

 

[eehelp150]

The first one is not a node equation. Vin is not an essential node, it is part of the reference supernode since it has a fixed potential with respect to the reference node.

The second equation is good. Solve it for V1.

The third equation is also good. Solve it for V2.

$R_3V_1-R_3V_{in}+R_1V_1=0$
$V_2+R_2C_1\dot{V_2}-R_2C_1\dot{V_{in}}$

$V_1=\frac{R_3V_{in}}{R_3+R_1}$
$V_2=R_2C_1(\dot{V_{in}}-\dot{V_2})$

$V_o=V_1-V_2$
$V_o=\frac{R_3V_{in}}{R_3+R_1}-R_2C_1(\dot{V_{in}}-\dot{V_2})$
How would I get rid of $\dot{V_2}$?

 

[gneill]

Please do not edit content out your previous posts. It makes followups discussing that content nonsensical. If you do edit a post, make sure that you leave a note in the post indicating what changes you made and why. It is best to have a policy of only adding to a previous post, not removing content. Fixing typos is fine.

$R_3V_1-R_3V_{in}+R_1V_1=0$
$V_2+R_2C_1\dot{V_2}-R_2C_1\dot{V_{in}}$

$V_1=\frac{R_3V_{in}}{R_3+R_1}$
$V_2=R_2C_1(\dot{V_{in}}-\dot{V_2})$

$V_o=V_1-V_2$
$V_o=\frac{R_3V_{in}}{R_3+R_1}-R_2C_1(\dot{V_{in}}-\dot{V_2})$
How would I get rid of $\dot{V_2}$?

Solve for V2 before you combine with V1. The V2 equation is a simple differential equation. Hint: What is $\dot{V_{in}}$?

 

[eehelp150]

Please do not edit content out your previous posts. It makes followups discussing that content nonsensical. If you do edit a post, make sure that you leave a note in the post indicating what changes you made and why. It is best to have a policy of only adding to a previous post, not removing content. Fixing typos is fine.
Solve for V2 before you combine with V1. The V2 equation is a simple differential equation. Hint: What is $\dot{V_{in}}$?

I edited that post on accident and didn't know how to undo. My bad.
$\frac{V_1-V_{in}}{R_1}+\frac{V_1}{R_3}=0$
$V_{in} = V_1(1+\frac{R_1}{R_3})$
$\dot{V_{in}}=\dot{V_1}(1+\frac{R_1}{R_3})$
$V_2=R_2C_1(\dot{V_1}(1+\frac{R_1}{R_3})-\dot{V_2})$

 

[gneill]

Question: Is Vin a DC source or an AC source?

 

[eehelp150]

Question: Is Vin a DC source or an AC source?

The problem was given like this as practice for the exam. I think the professor said something about Vin being an AC sinusoid for the exam. Also the prompt for this problem is "Find the differential equation for Vo". I forgot to include that in the OP.

 

[gneill]

The problem was given like this as practice for the exam. I think the professor said something about Vin being an AC sinusoid for the exam. Also the prompt for this problem is "Find the differential equation for Vo". I forgot to include that in the OP.

I see. That makes things a bit trickier. I don't think you can eliminate V2' without using the actual function for Vin. I suppose you could write V2 in terms of Vo, since Vo = V1 - V2. That would at least lead to a differential equation for Vo.

 

[eehelp150]

I see. That makes things a bit trickier. I don't think you can eliminate V2' without using the actual function for Vin. I suppose you could write V2 in terms of Vo, since Vo = V1 - V2. That would at least lead to a differential equation for Vo.

What if $V_{in}$ was sin(t)?
How would I go about solving?

 

[gneill]

If you have the actual function then you have its derivative, too. You can plug those into your V2 node equation and solve the differential equation. But that would lead to the overall solution, not the differential equation for Vo.

 

[eehelp150]

If you have the actual function then you have its derivative, too. You can plug those into your V2 node equation and solve the differential equation. But that would lead to the overall solution, not the differential equation for Vo.

What do you mean for overall solution? Is that not the differential equation for Vo?
How would I get Vo in terms of Vin? I don't see how to eliminate V2, even with a function for Vin

 

[gneill]

What do you mean for overall solution? Is that not the differential equation for Vo?

It would be the time domain solution for Vo. Some combination of sine and cosine functions.

How would I get Vo in terms of Vin? I don't see how to eliminate V2, even with a function for Vin

You make the substitution for V2 that I suggested using Vo = V1 - V2. Then V2 becomes V1 - Vo, and you already have V1 in terms of Vin.

 

[eehelp150]

It would be the time domain solution for Vo. Some combination of sine and cosine functions.

You make the substitution for V2 that I suggested using Vo = V1 - V2. Then V2 becomes V1 - Vo, and you already have V1 in terms of Vin.

This look good?
$V_1=\frac{R_3V_{in}}{R_3+R_1}$

$V_2=R_2C_1(\dot{V_{in}}-\dot{V_2})$

$V_O=V_1-V_2$
$V_2=V_O-V_1$
$\dot{V_1}=\frac{R_3\dot{V_{in}}}{R_3+R_1}$
$\dot{V_2}=\dot{V_O}-\dot{V_1}$

$V_2=R_2C_1(\dot{V_{in}}-\dot{V_2})$
$V_O-\frac{R_3V_{in}}{R_3+R_1}=R_2C_1(\dot{V_{in}}-(\dot{V_O}-\frac{R_3\dot{V_{in}}}{R_3+R_1}))$

 

[gneill]

Yes, that's what I meant.

 

[eehelp150]

Yes, that's what I meant.

There is only one energy storage element in this circuit so there is no dampening right? Would tau simply be Rth*C? Where Rth = R1+R2+R3?

 

[gneill]

There is only one energy storage element in this circuit so there is no dampening right? Would tau simply be Rth*C? Where Rth = R1+R2+R3?

There will be dampening if there are transients that die out due to the resistance in the circuit. Transients will occur if the driving source Vin is discontinuous in some way (such as if the signal is suddenly applied when it is at a non-zero part of its cycle). Dampening in single reactor circuits are characterized by a $\tau$ that is the time constant for the exponential decay of the transients.

If you are determining the Rth that the capacitor "sees", then you should re-draw what the circuit looks like with the source suppressed. I think you'll find that R1 and R3 can play no role.

I thought that Vin was an AC source and that you'd be looking at the steady-state (driven) solution, no? Is there some part of the problem statement that we haven't seen?

 

[eehelp150]

There will be dampening if there are transients that die out due to the resistance in the circuit. Transients will occur if the driving source Vin is discontinuous in some way (such as if the signal is suddenly applied when it is at a non-zero part of its cycle). Dampening in single reactor circuits are characterized by a $\tau$ that is the time constant for the exponential decay of the transients.

If you are determining the Rth that the capacitor "sees", then you should re-draw what the circuit looks like with the source suppressed. I think you'll find that R1 and R3 can play no role.

I thought that Vin was an AC source and that you'd be looking at the steady-state (driven) solution, no? Is there some part of the problem statement that we haven't seen?

R1 and R3 play no role because they are shorted when the source is shorted, correct?

There is no problem statement, the teacher simply told us to solve this as is for practice. He said there will be an AC source and numerical values for resistors and capacitor on the exam.

 

[gneill]

R1 and R3 play no role because they are shorted when the source is shorted, correct?

Right.

There is no problem statement, the teacher simply told us to solve this as is for practice. He said there will be an AC source and numerical values for resistors and capacitor on the exam.

I can see deriving the differential equation on an exam, but solving it as well seems ambitious.

 

[The Electrician]

This look good?
$V_1=\frac{R_3V_{in}}{R_3+R_1}$

$V_2=R_2C_1(\dot{V_{in}}-\dot{V_2})$

$V_O=V_1-V_2$
$V_2=V_O-V_1$ This should be: $V_2=V_1-V_O$
$\dot{V_1}=\frac{R_3\dot{V_{in}}}{R_3+R_1}$
$\dot{V_2}=\dot{V_O}-\dot{V_1}$ This should be: $\dot{V_2}=\dot{V_1}-\dot{V_O}$

$V_2=R_2C_1(\dot{V_{in}}-\dot{V_2})$
$V_O-\frac{R_3V_{in}}{R_3+R_1}=R_2C_1(\dot{V_{in}}-(\dot{V_O}-\frac{R_3\dot{V_{in}}}{R_3+R_1}))$

You made a silly error as indicated above. 10 points off!

The reason I noticed this is because I worked the problem using the Laplace variable s, and didn't get the same result you did.