SUCRALOSE
- 12
- 1
I have tried everything on this one that I can think of.
I understand that the forces in the horizontal are 0, but I don't know where to start.
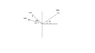
says: determine the angle for which the resultant of the three forces is vertical. See Picture.
I understand that the forces in the horizontal are 0, but I don't know where to start.
says: determine the angle for which the resultant of the three forces is vertical. See Picture.