vantz
- 13
- 0
1.
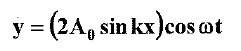
2.
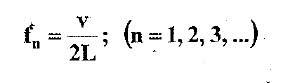
3.
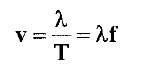
4. [PLAIN]http://img176.imageshack.us/img176/7186/34581263.jpg
5. [PLAIN]http://img87.imageshack.us/img87/8069/16289518.jpg [/PLAIN]
6. [PLAIN]http://img291.imageshack.us/img291/5840/49412218.jpg [/PLAIN]
7. [PLAIN]http://img809.imageshack.us/img809/8945/20137696.jpg [/PLAIN]
8. [PLAIN]http://img99.imageshack.us/img99/7555/78954615.jpg
2.
3.
4. [PLAIN]http://img176.imageshack.us/img176/7186/34581263.jpg
5. [PLAIN]http://img87.imageshack.us/img87/8069/16289518.jpg [/PLAIN]
6. [PLAIN]http://img291.imageshack.us/img291/5840/49412218.jpg [/PLAIN]
7. [PLAIN]http://img809.imageshack.us/img809/8945/20137696.jpg [/PLAIN]
8. [PLAIN]http://img99.imageshack.us/img99/7555/78954615.jpg
Last edited by a moderator: