paalfis
- 69
- 2
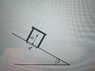
http://file://localhost/Users/pablotano_94/Downloads/IMG_20141205_183228102.jpg 1. Homework Statement
Assume that the friction coefficient (both static and dynamic) is ¨u¨.
a) What is the maximum slope yo can get in order that the bench does not slide?
b) What is the maximum slope yo can get in order that the bench does not turn?
c) What condition must be satisfied, while you are increasing the slope, in order that the bench turns but does not slide?
My results where:
a)m*g*sin(B)<mgcos(B)*u
b)tan(B)<d/(2h)
c) u*m*g*cos(arctan(d/(2h))>m*g*sin(B)
This problem is supposed to be a tough one.. But my solution was quite simple, so, I think I am missing something, I really need some help with this one..
Thanks!
Assume that the friction coefficient (both static and dynamic) is ¨u¨.
a) What is the maximum slope yo can get in order that the bench does not slide?
b) What is the maximum slope yo can get in order that the bench does not turn?
c) What condition must be satisfied, while you are increasing the slope, in order that the bench turns but does not slide?
The Attempt at a Solution
My results where:
a)m*g*sin(B)<mgcos(B)*u
b)tan(B)<d/(2h)
c) u*m*g*cos(arctan(d/(2h))>m*g*sin(B)
This problem is supposed to be a tough one.. But my solution was quite simple, so, I think I am missing something, I really need some help with this one..
Thanks!
Attachments
Last edited by a moderator: