What are the cord tension and force on the hinge for this angled beam?

[hangingwire]

Homework Statement

Find cord tension and force on the hinge on this beam given the following:

Picture of the equation (in attachments)
beam is 10 kg
beam is 8.0m long

Homework Equations

[T=0
[F=0

[h2]The Attempt at a Solution[/h2]

Finding the Torque on the wire...
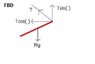
I attached my FBD I drew. Before I start, one question? Since the beam is on an angle, would there be a horizontal force on the x-axis resulting from the Mass of the beam? If so, It could be 60 degrees? Mg Sin60?

That is my attempt using the "Z-rule" in angles

Anyways:

[T= 0
Tcw = Tccw
mg(d) = Tsin( ) * (d)
(10)(9.8)(4) = T sin30 * (8m) ----> Sin 30* given that directly across is 90 degrees + 60 degrees given = 30 degrees left at where the beam and wire are attached.

392N = T sin30 * (8m)

392N divided by 8m = 49

49 = T sin30

49 divided by sin30 --> 98?

The answer is 49N. Why did I get double the answer? Is there something with my angles?

 

[voko]

The weight of the beam acts at angle to the "arm", so its torque must involve the sine of the angle. Intuitively that should be fairly clear: the "more vertical" the beam gets, the easier it is to hold it in place.

 

[hangingwire]

So instead of "Mg" just being "Mg". It is "Mgsin(30)"? Is that what you are trying to say? If I change that in my equation it works out?

If that is the case, waste no time to say... Would the horizontal axis on Mg also require a MgCos(30) to workout the force from the hinge in components?

 

[voko]

It should be fairly obvious that 49 sin 30 = T sin 30 implies T = 49.

Regarding the forces, the answer is no. If you you use the horizontal and vertical axes, then the weight is purely vertical - it always is; the other forces, however, are not.

 

[hangingwire]

Figured it out! Thanks