What Are the Electrical Characteristics of the Circuit in Figure 27-40?

[Zonda]

Please help!

My problem is: (with figure attached, the figure explains the majority of the ptorblem)
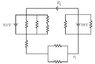
(a) What is the size and direction of current i1 in Fig. 27-40, where each resistance is 2.2 and V1 = 18 V?

(b) What is the power of the 18 V battery, and is energy being supplied or absorbed by the battery?

(c) What is the power of the 10 V battery, and is energy being supplied or absorbed by the battery?

(d) What is the power of the 5.0 V battery, and is energy being supplied or absorbed by the battery?

Relevant Equations
V=iR

For part (a) I'm having trouble firguring out which resistances to use. Do I use all of the resistances and add them up according to whether they are parallel or perpendicular? Then, when I get the resistance that I need, do I just use the 10 V battery as my voltage to calculate the current? I tried adding all of the resistances and I got 8.64 ohms. Is this correct?

For part (b) I need to know again what resistance to use to calculate the current, which I would need to calculate power. If I can get some help on (b), I can probably do (c) and (d) by myself.

 

[member 553083]

Answer:Part (a): The total resistance of the circuit is 8.64 ohms. To calculate the current, use Ohm's Law: V = iR, so i1 = V1/R = 18V/8.64Ω = 2.08 A. The direction of the current is clockwise around the circuit, as indicated by the arrows in the figure. Part (b): To calculate the power of the 18 V battery, we need to calculate the current through the battery. To do this, the resistances in parallel with the battery must be added together to get a total resistance. This is 5.6 ohms. Then, using Ohm's Law again, i = V/R = 18V/5.6Ω = 3.21A. The power of the battery is P = V*i = 18V*3.21A = 58.38W. This means that energy is being supplied by the battery. Part (c): To calculate the power of the 10 V battery, we need to calculate the current through the battery. To do this, the resistances in parallel with the battery must be added together to get a total resistance. This is 2.2 ohms. Then, using Ohm's Law again, i = V/R = 10V/2.2Ω = 4.55A. The power of the battery is P = V*i = 10V*4.55A = 45.5W. This means that energy is being supplied by the battery. Part (d): To calculate the power of the 5 V battery, we need to calculate the current through the battery. To do this, the resistances in parallel with the battery must be added together to get a total resistance. This is 1.1 ohms. Then, using Ohm's Law again, i = V/R = 5V/1.1Ω = 4.55A. The power of the battery is P = V*i = 5V*4.55A = 22.75W. This means that energy is being supplied by the battery.